题目内容
函数 在点
在点 处有极值,则
处有极值,则 的单调增区间是
的单调增区间是
 在点
在点 处有极值,则
处有极值,则 的单调增区间是
的单调增区间是A. | B. | C. | D. 和 和 |
D
试题分析:
 ,
,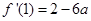 。由于函数
。由于函数 在点
在点 处有极值,所以
处有极值,所以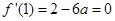 ,解得
,解得 ,所以
,所以 ,
,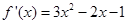 。当
。当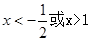 时,
时,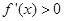 ,所以
,所以 的单调增区间是
的单调增区间是 和
和 。故选D
。故选D点评:求函数的单调区间常结合导数,求解的过程要用到的结论是:若
 ,则函数
,则函数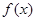 在
在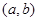 上为增函数,
上为增函数,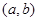 为增区间;若
为增区间;若 ,则函数函数
,则函数函数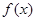 在
在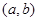 上为减函数,
上为减函数,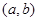 为减区间。
为减区间。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
 在点
在点 处有极值,则
处有极值,则 的单调增区间是
的单调增区间是A. | B. | C. | D. 和 和 |
 ,
,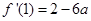 。由于函数
。由于函数 在点
在点 处有极值,所以
处有极值,所以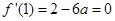 ,解得
,解得 ,所以
,所以 ,
,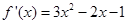 。当
。当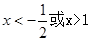 时,
时,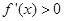 ,所以
,所以 的单调增区间是
的单调增区间是 和
和 。故选D
。故选D ,则函数
,则函数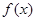 在
在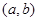 上为增函数,
上为增函数,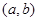 为增区间;若
为增区间;若 ,则函数函数
,则函数函数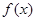 在
在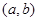 上为减函数,
上为减函数,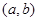 为减区间。
为减区间。
 阅读快车系列答案
阅读快车系列答案