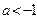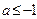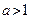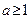题目内容
(12分)已知函数f(x)=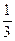 ax3-bx2 +(2-b)x+1,在x=x2处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2。
ax3-bx2 +(2-b)x+1,在x=x2处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2。
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围。
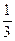 ax3-bx2 +(2-b)x+1,在x=x2处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2。
ax3-bx2 +(2-b)x+1,在x=x2处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2。(1)证明:a>0;
(2)若z=a+2b,求z的取值范围。
(1)见解析(2)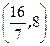
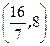
求函数f′(x)的导数f′(x)=ax2-2bx+2-b
(1)由函数f(x)在x=x1处取得极大值,在x=x2处取得极小值,知x1,x2是f’(x)=0的两个根。所以f’(x)=a(x-x1)(x-x2)
当x<x1时,f(x)为增函数,f′(x)>0,由x-x1<0,x- x2<0得a>0
x2<0得a>0
(2)在题设下,0<x1<1<x2<2等价于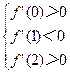 即
即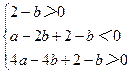
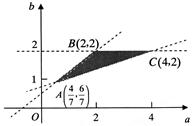
化简得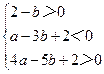 此不等式组表示的区域为平面aob上三条直线:2-b=0,a-3b+2=0,4a-5b+2=0,所围成的
此不等式组表示的区域为平面aob上三条直线:2-b=0,a-3b+2=0,4a-5b+2=0,所围成的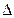 ABC的内部,其三个顶点分别为:A
ABC的内部,其三个顶点分别为:A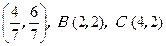 .
.
在这三点的值依次为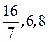
 ,所以z的取值范围为
,所以z的取值范围为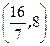

(1)由函数f(x)在x=x1处取得极大值,在x=x2处取得极小值,知x1,x2是f’(x)=0的两个根。所以f’(x)=a(x-x1)(x-x2)
当x<x1时,f(x)为增函数,f′(x)>0,由x-x1<0,x-
 x2<0得a>0
x2<0得a>0(2)在题设下,0<x1<1<x2<2等价于
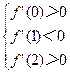 即
即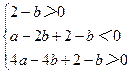
化简得
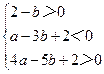 此不等式组表示的区域为平面aob上三条直线:2-b=0,a-3b+2=0,4a-5b+2=0,所围成的
此不等式组表示的区域为平面aob上三条直线:2-b=0,a-3b+2=0,4a-5b+2=0,所围成的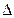 ABC的内部,其三个顶点分别为:A
ABC的内部,其三个顶点分别为:A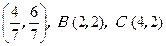 .
.在这三点的值依次为
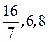
 ,所以z的取值范围为
,所以z的取值范围为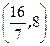

练习册系列答案
相关题目
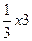 +bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。
+bx2+cx+bc,其导函数为f+(x)。令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M。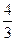 ,试确定b、c的值;
,试确定b、c的值;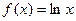
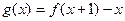 的最大值;
的最大值; 时,求证
时,求证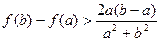 ;
;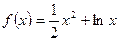
 为
为 的极值点,求实数
的极值点,求实数 的值
的值 是函数
是函数 的一个零点, 且
的一个零点, 且 , 其中
, 其中 , 则求
, 则求 的值
的值 时
时 ,求
,求 的取值范围
的取值范围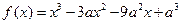 .
.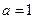 ,求函数
,求函数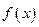 的极值;
的极值;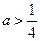 ,且当
,且当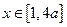 时,
时,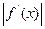
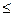 12a恒成立,试确定
12a恒成立,试确定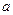 的取值范围.
的取值范围. 在点
在点 处有极值,则
处有极值,则 的单调增区间是
的单调增区间是


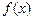 的导数
的导数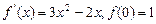 .求函数
.求函数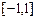 上的最小值与最大值.
上的最小值与最大值.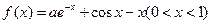 若对任意的
若对任意的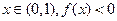 恒成立,则
恒成立,则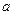 的取值范围( )
的取值范围( )