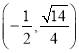题目内容
【题目】设函数![]() 的定义域为
的定义域为![]() ,若满足条件:存在
,若满足条件:存在![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则称
,则称![]() 为“倍缩函数”.若函数
为“倍缩函数”.若函数![]() 为“倍缩函数”,则实数
为“倍缩函数”,则实数![]() 的取值范围是
的取值范围是
A. (﹣∞,ln2﹣1) B. (﹣∞,ln2﹣1]
C. (1﹣ln2,+∞) D. [1﹣ln2,+∞)
【答案】C
【解析】∵函数f(x)=lnx+t为“倍缩函数”,
且满足存在[a,b]D,使f(x)在[a,b]上的值域是[![]() ],
],
∴f(x)在[a,b]上是增函数;
∴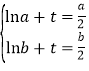 , 即
, 即![]() 在(0,+∞)上有两根,
在(0,+∞)上有两根,
即y=t和g(x)=![]() ﹣lnx在(0,+∞)有2个交点, g′(x)=
﹣lnx在(0,+∞)有2个交点, g′(x)=![]() ,
,
令g′(x)>0,解得:x>2,
令g′(x)<0,解得:0<x<2,
故g(x)在(0,2)递减,在(2,+∞)递增,
故g(x)≥g(2)=1﹣ln2,故t>1﹣ln2, 故选C:.

练习册系列答案
相关题目