题目内容
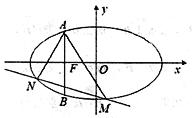
【题目】如图，在平面直角坐标系xOy中，过点A（﹣6，0）的直线l1与直线l2：y=2x相交于点B（m，4）．
（1）求直线l1的表达式；
（2）过动点P（n，0）且垂于x轴的直线与l1 ， l2的交点分别为C，D，当点C位于点D上方时，写出n的取值范围．
【答案】
（1）
解：∵点B在直线l2上，
∴4=2m，
∴m=2，点B（2，4）
设直线l1的表达式为y=kx+b，
由题意 
，解得 
，
∴直线l1的表达式为y= 
x+3．
（2）
解：与图象可知n＜2．
【解析】不同考查两条直线平行、相交问题，解题的关键是灵活应用待定系数法，学会利用图象根据条件确定自变量取值范围．
（1）先求出点B坐标，再利用待定系数法即可解决问题；
（2）由图象可知直线l1在直线l2上方即可，由此即可写出n的范围．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计，随机抽取
名学生作为样本，得到这
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |
（1）求出表中
及图中
的值；
（2）试估计他们参加社区服务的平均次数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至少1人参加社区服务次数在区间
内的概率.
【题目】毕节市正实施“五城同创”计划。为搞好卫生维护工作，政府招聘了200名市民志愿者，按年龄情况进行统计的频率分布表和频率分布直方图如下：
分组（岁） | 频数 | 频率 |
[30,35) | 20 | 0.1 |
[35,40) | 20 | 0.1 |
[40,45) | ① | 0.2 |
[45,50) | ② | ③ |
[50,55] | 40 | 0.2 |
合计 | 200 | 1 |
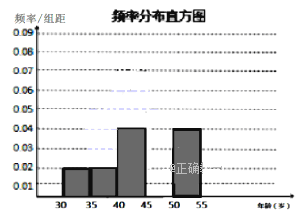
(1)频率分布表中的①②③位置应填什么数？补全频率分布直方图；
(2)根据频率分布直方图估计这200名志愿者的平均年龄．
