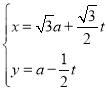题目内容
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天内记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:

若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若以每组的中点代表该组数据值,求这100小时内每小时的平均降雨量;
(2)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.再从这10小时中随机抽取3小时,求抽取的这3小时中属于一级警戒时间的分布列与数学期望.
【答案】(1)87.25![]() ; (2)
; (2)![]() 小时,见解析.
小时,见解析.
【解析】
(1)先分别算出五组数据数据对应的频率,再利用平均数公式求解.
(2)先根据频率分布直方图得到一级警戒和二级警戒的时间数,用![]() 表示一级警戒的小时数,列出
表示一级警戒的小时数,列出![]() 的可能取值,再分别求得其概率,列出分布列,然后代入期望公式求解.
的可能取值,再分别求得其概率,列出分布列,然后代入期望公式求解.
(1)这五组数据对应的频率分别为:0.05,0.35,0.3,0.2,0.1.
故这100小时的平均降雨量为:
0.05×77.5+0.35×82.5+0.3×87.5+0.2×92.5+0.1×97.5=87.25![]() .
.
(2)由频率分步直方图可知,属于一级警戒的频率为:(0.04+0.02)×5=0.3,
则属于二级警戒的频率为1-0.3=0.7.所以,抽取的这10个小时中,
属于一级警戒的有3小时,属于二级警戒的有7小时.
从这10小时中抽取3小时,用![]() 表示一级警戒的小时数,
表示一级警戒的小时数,![]() 的取值可能为0,1,2,3.
的取值可能为0,1,2,3.
则![]() ,,
,,![]() .
.
所以,![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
则![]() 的期望值为:
的期望值为:![]() (小时).
(小时).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() 倍B.
倍B.![]() 倍C.
倍C.![]() 倍D.
倍D.![]() 倍
倍
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):

若分数不低于95分,则称该员工的成绩为“优秀”.
(1)从这20人中任取3人,求恰有1人成绩“优秀”的概率;
(2)根据这20人的分数补全下方的频率分布表和频率分布直方图,并根据频率分布直方图解决下面的问题.
组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
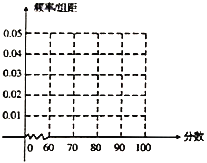
①估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表);
②若从所有员工中任选3人,记![]() 表示抽到的员工成绩为“优秀”的人数,求
表示抽到的员工成绩为“优秀”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.