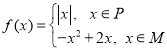题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() 时,
时,![]() 在
在![]() 单调递增;
单调递增;![]() 时,
时,![]() 在区间
在区间![]() ,
,![]() 单调递增;在区间
单调递增;在区间![]() 单调递减.(2)见解析
单调递减.(2)见解析
【解析】
(1)求出导函数![]() ,然后根据方程
,然后根据方程![]() 的判别式得到导函数的符号,进而得到函数的单调性;(2)由题意得到方程
的判别式得到导函数的符号,进而得到函数的单调性;(2)由题意得到方程![]() 有两个根
有两个根![]() ,故可得
,故可得![]() ,且
,且![]() .然后可得
.然后可得![]() ,最后利用导数可证得
,最后利用导数可证得![]() ,从而不等式成立.
,从而不等式成立.
(1)∵![]() ,
,
∴![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增;
单调递增;
②当![]() ,即
,即![]() 时,
时,
令![]() ,得
,得![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
∴![]() 单调递增区间为
单调递增区间为![]() ,
,![]() ;
;
单调递减区间为![]() .
.
综上所述:当![]() 时,
时,![]() 在
在![]() 单调递增;
单调递增;
![]() 时,
时,![]() 在区间
在区间![]() ,
,![]() 单调递增;在区间
单调递增;在区间![]() 单调递减.
单调递减.
(2)由(1)得![]() .
.
∵函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,
,
∴方程![]() 有两个根
有两个根![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,解得
,解得![]() .
.
由题意得![]()
![]()
![]()
![]()
![]() .
.
令![]() ,
,
则![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
,
∴![]() .
.

 天天向上口算本系列答案
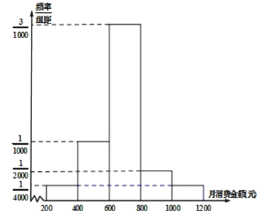
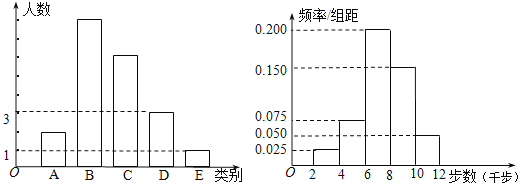
天天向上口算本系列答案【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,大学生
推出的多款健康运动软件中的一款,大学生![]() 的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:
的微信好友中有400位好友参与了“微信运动”.他随机抽取了40位参与“微信运动”的微信好友(女20人,男20人)在某天的走路步数,经统计,其中女性好友走路的步数情况可分为五个类别:![]() 、0~2000步,(说明:“0~2000”表示“大于或等于0,小于2000”,以下同理),
、0~2000步,(说明:“0~2000”表示“大于或等于0,小于2000”,以下同理),![]() 、2000~5000步,
、2000~5000步,![]() 、5000~8000步,
、5000~8000步,![]() 、8000~10000步,
、8000~10000步,![]() 、10000~12000步,且
、10000~12000步,且![]() 三种类别的人数比例为
三种类别的人数比例为![]() ,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
,将统计结果绘制如图所示的柱形图;男性好友走路的步数数据绘制如图所示的频率分布直方图.
参与者 | 超越者 | 合计 | |
男 | 20 | ||
女 | 20 | ||
合计 | 40 |
若某人一天的走路步数大于或等于8000,则被系统认定为“超越者”,否则被系统认定为“参与者”.
(Ⅰ)若以大学生![]() 抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生
抽取的微信好友在该天行走步数的频率分布,作为参与“微信运动”的所有微信好友每天走路步数的概率分布,试估计大学生![]() 的参与“微信运动”的400位微信好友中,每天走路步数在
的参与“微信运动”的400位微信好友中,每天走路步数在
(Ⅱ)若在大学生![]() 该天抽取的步数在8000~12000的微信好友中,按男女比例分层抽取9人进行身体状况调查,然后再从这9位微信好友中随机抽取4人进行采访,求其中至少有一位女性微信好友被采访的概率;
该天抽取的步数在8000~12000的微信好友中,按男女比例分层抽取9人进行身体状况调查,然后再从这9位微信好友中随机抽取4人进行采访,求其中至少有一位女性微信好友被采访的概率;
(Ⅲ)请根据抽取的样本数据完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() 的把握认为“认定类别”与“性别”有关?
的把握认为“认定类别”与“性别”有关?