题目内容
在平面直角坐标系xOy中,已知对于任意实数k,直线( k+1)x+(k-
k+1)x+(k- )y-(3k+
)y-(3k+ )=0恒过定点F.设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为2+
)=0恒过定点F.设椭圆C的中心在原点,一个焦点为F,且椭圆C上的点到F的最大距离为2+ .
.
(1)求椭圆C的方程;
(2)设(m,n)是椭圆C上的任意一点,圆O:x2+y2=r2(r>0)与椭圆C有4个相异公共点,试分别判断圆O与直线l1:mx+ny=1和l2:mx+ny=4的位置关系.
(1)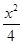 +y2=1.(2)直线l1与圆O相交,直线l2与圆O相离.
+y2=1.(2)直线l1与圆O相交,直线l2与圆O相离.
解析

练习册系列答案
相关题目
 ),且长轴长与短轴长的比是
),且长轴长与短轴长的比是
 =1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x-
=1(a>b>0)的短半轴长,椭圆E的右焦点F在圆O内,且到直线l:y=x- 的距离为
的距离为 -
- ,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆O的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
 和定直线
和定直线 ,动点与定点
,动点与定点 的距离等于点
的距离等于点 到定直线
到定直线 的距离,记动点
的距离,记动点 .
. 为圆心的圆与曲线
为圆心的圆与曲线 、
、 不同两点,且线段
不同两点,且线段 是此圆的直径时,求直线
是此圆的直径时,求直线 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的短轴长。
的短轴长。 与
与 轴的交点为
轴的交点为 ,过坐标原点
,过坐标原点 的直线
的直线 与
与 ,直线
,直线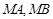 分别与
分别与 。
。
 。
。 的面积分别为
的面积分别为 ,若
,若 ,求
,求 的取值范围。
的取值范围。 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点为
,右焦点为 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 ,线段
,线段 垂直平分线交
垂直平分线交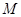 ,求点
,求点 的方程;
的方程; 轴交于点
轴交于点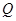 ,不同的两点
,不同的两点 在
在 ,求
,求 的取值范围.
的取值范围.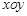 中,动点
中,动点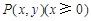 满足:点
满足:点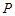 到定点
到定点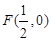 与到
与到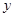 轴的距离之差为
轴的距离之差为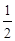 .记动点
.记动点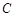 .
. 的直线交曲线
的直线交曲线 、
、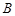 两点,过点
两点,过点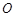 的直线交直线
的直线交直线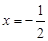 于点
于点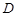 ,求证:直线
,求证:直线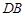 平行于
平行于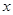 轴.
轴.