题目内容
3. 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C.(Ⅰ)求证:B1C⊥AC1;
(Ⅱ)设点E,F分别是B1C,AA1的中点,试判断直线EF与平面ABC的位置关系,并说明理由;
(Ⅲ)求二面角B-AC1-C的余弦值.
分析 (Ⅰ)根据线面垂直的性质定理即可证明B1C⊥AC1;
(Ⅱ)根据线面平行的判定定理即可判断直线EF与平面ABC的位置关系;
(Ⅲ)建立空间坐标系,求出平面的法向量,利用向量法进行求解即可.
解答  证明:(Ⅰ)连接BC1.
证明:(Ⅰ)连接BC1.
在正方形ABB1A1中,AB⊥BB1.
因为 平面AA1B1B⊥平面BB1C1C,平面AA1B1B∩平面BB1C1C=BB1,AB?平面ABB1A1,
所以 AB⊥平面BB1C1C.…(1分)
因为 B1C?平面BB1C1C,
所以 AB⊥B1C.…(2分)
在菱形BB1C1C中,BC1⊥B1C.
因为 BC1?平面ABC1,AB?平面ABC1,BC1∩AB=B,
所以 B1C⊥平面ABC1.…(4分)
因为 AC1?平面ABC1,
所以 B1C⊥AC1.…(5分)
(Ⅱ)EF∥平面ABC,理由如下:…(6分)
取BC的中点G,连接GE,GA.
因为 E是B1C的中点,
所以 GE∥BB1,且GE=$\frac{1}{2}B{B_1}$.
因为 F是AA1的中点,
所以 AF=$\frac{1}{2}A{A_1}$.
在正方形ABB1A1中,AA1∥BB1,AA1=BB1.
所以 GE∥AF,且GE=AF.
所以 四边形GEFA为平行四边形.
所以 EF∥GA.…(8分)
因为 EF?平面ABC,GA?平面ABC,
所以 EF∥平面ABC.…(9分)
(Ⅲ)在平面BB1C1C内过点B作Bz⊥BB1.
由(Ⅰ)可知:AB⊥平面BB1C1C.以点B为坐标原点,分别以BA,BB1所在的直线为x,y轴,建立如图所示的空间直角坐标系B-xyz,设A(2,0,0),则B1(0,2,0).
在菱形BB1C1C中,∠BB1C1=60°,所以 $C(0,-1,\sqrt{3})$,${C_1}(0,1,\sqrt{3})$.
设平面ACC1的一个法向量为n=(x,y,1).
因为 $\left\{\begin{array}{l}n•\overrightarrow{AC}=0\\ n•\overrightarrow{C{C_1}}=0\end{array}\right.$即$\left\{\begin{array}{l}(x,y,1)•(-2,-1,\sqrt{3})=0\\(x,y,1)•(0,2,0)=0\end{array}\right.$
所以 $\left\{\begin{array}{l}x=\frac{{\sqrt{3}}}{2}\\ y=0\end{array}\right.$即$n=(\frac{{\sqrt{3}}}{2},0,1)$.…(11分)
由(Ⅰ)可知:$\overrightarrow{C{B_1}}$是平面ABC1的一个法向量.…(12分)
所以 $cos<n,\overrightarrow{C{B_1}}>=\frac{{n•\overrightarrow{C{B_1}}}}{{|n|•|{\overrightarrow{C{B_1}}}|}}=\frac{{(\frac{{\sqrt{3}}}{2},0,1)•(0,3,-\sqrt{3})}}{{\sqrt{\frac{3}{4}+1}•\sqrt{9+3}}}=-\frac{{\sqrt{7}}}{7}$.
所以 二面角B-AC1-C的余弦值为$\frac{{\sqrt{7}}}{7}$.…(14分)
点评 本题主要考查空间直线和平面之间的位置关系的判断,以及二面角的求解,要求熟练掌握相应的判定定理,利用向量法是解决二面角的常用方法,考查学生的运算和推理能力.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
]与函数g(x)=ax2+bx的图象恰有1个公共点,则a,b的取值不可能是( )
| A. | a=5,b=1 | B. | a=4,b=-1 | C. | a=-2,b=-1 | D. | a=-4,b=1 |
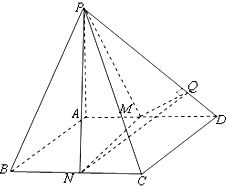 如图,已知四棱锥P-ABCD,底面是边长为2的正方形,PA⊥底面ABCD,M、N分别为AD、BC的中点,MQ⊥PD于Q,直线PC与平面PBA所成的角的正弦为$\frac{\sqrt{3}}{3}$.
如图,已知四棱锥P-ABCD,底面是边长为2的正方形,PA⊥底面ABCD,M、N分别为AD、BC的中点,MQ⊥PD于Q,直线PC与平面PBA所成的角的正弦为$\frac{\sqrt{3}}{3}$.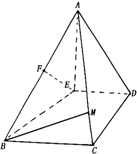 如图,在棱锥A-BCDE中,平面ABE上平面BCDE,BE⊥AE,BE⊥ED,ED∥BC,BC=BE=EA=2,DE=1.
如图,在棱锥A-BCDE中,平面ABE上平面BCDE,BE⊥AE,BE⊥ED,ED∥BC,BC=BE=EA=2,DE=1.