Question

8．已知F₁、F₂分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1 （a＞b＞0）的左右焦点，P是椭圆上任一点，从焦点F₂引∠F₁PF₂的外角平分线的垂线，垂足为Q，则Q点轨迹为以原点为圆心，a为半径的圆．

Answer 1

分析 延长F₁P，与F₂Q的延长线交于M点，连接QO，根据等腰三角形“三线合一”和三角形中位线定理，结合椭圆的定义证出OQ的长恰好等于椭圆的长半轴a，得动点Q的轨迹方程为x²+y²=a²，从而解得．

解答 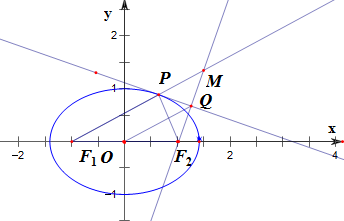解：由题意，延长F₁P，与F₂Q的延长线交于M点，连接QO，
∵PQ是∠F₂PM的平分线，且PQ⊥MF₂；
∴△F₂MP中，|PF₂|=|PM|且Q为MF₂的中点，
由三角形中位线定理，得|OQ|=$\frac{1}{2}$|MF₁|=$\frac{1}{2}$（|MP|+|PF₁|）
∵由椭圆的定义，得|PF₁|+|PF₂|=2a，（2a是椭圆的长轴）；
可得|MP|+|PF₁|=2a，
∴|OQ|=$\frac{1}{2}$（|MP|+|PF₁|）=a，可得动点Q的轨迹方程为x²+y²=a²
∴点Q的轨迹为以原点为圆心，a为半径的圆．
故答案为：以原点为圆心，a为半径的圆．

点评 本题在椭圆中求动点Q的轨迹，着重考查了椭圆的定义、等腰三角形的判定和三角形中位线定理等知识，属于中档题．