题目内容
15.中心在原点的椭圆C关于坐标轴对称,点B(0,1)是椭圆C的一个短轴端点,点P,Q在椭圆C运动,若椭圆C的离心率为$\frac{\sqrt{2}}{2}$,且△BPQ的垂心恰好为椭圆C的右焦点,求直线PQ的方程.分析 由题意可求得椭圆方程为$\frac{{x}^{2}}{2}$+y2=1;再设直线PQ的方程为y=x+k,P(x1,y1),Q(x2,y2);从而可得x1+x2=-$\frac{4k}{3}$,x1x2=$\frac{2{k}^{2}-2}{3}$,再构造向量$\overrightarrow{BQ}$=(x2,y2-1),$\overrightarrow{FP}$=(x1-1,y1);从而化简求得k=1或k=-$\frac{4}{3}$;再检验即可.
解答 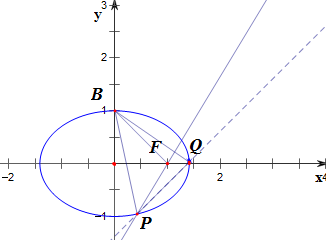 解:由题意,b=1,
解:由题意,b=1,
又∵e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
∴a=$\sqrt{2}$,c=1;
故椭圆方程为$\frac{{x}^{2}}{2}$+y2=1;
∵△BPQ的垂心恰好为椭圆C的右焦点F(1,0);
∴设直线PQ的方程为y=x+k,
设P(x1,y1),Q(x2,y2);
则由$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=x+k}\end{array}\right.$得,
3x2+4kx+2k2-2=0,
△=(4k)2-4×3×(2k2-2)>0,
故-$\sqrt{3}$<k<$\sqrt{3}$;
x1+x2=-$\frac{4k}{3}$,x1x2=$\frac{2{k}^{2}-2}{3}$,
又∵$\overrightarrow{BQ}$=(x2,y2-1),$\overrightarrow{FP}$=(x1-1,y1);
∴x2(x1-1)+(y2-1)y1=0,
即2x2x1+(k-1)(x2+x1)+k(k-1)=0,
即2$\frac{2{k}^{2}-2}{3}$-(k-1)$\frac{4k}{3}$+k(k-1)=0,
化简得,(k-1)(3k+4)=0;
故k=1或k=-$\frac{4}{3}$;
经检验,当k=1时,B,P,Q三点重合,无解;
故k=-$\frac{4}{3}$;
故直线PQ的方程为y=x-$\frac{4}{3}$.
即3x-3y-4=0.
点评 本题考查了椭圆与直线的位置关系及其应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 圆的一部分 | B. | 椭圆的一部分 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C. 如图,ABCD为正方形,BDEF为矩形,AB=2BF,DE⊥平面ABCD,G为EF中点.
如图,ABCD为正方形,BDEF为矩形,AB=2BF,DE⊥平面ABCD,G为EF中点. 如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.