题目内容
【题目】随着银行业的不断发展，市场竞争越来越激烈，顾客对银行服务质量的要求越来越高，银行为了提高柜员员工的服务意识，加强评价管理，工作中让顾客对服务作出评价，评价分为满意、基本满意、不满意三种．某银行为了比较顾客对男女柜员员工满意度评价的差异，在下属的四个分行中随机抽出40人（男女各半）进行分析比较．对40人一月中的顾客评价“不满意”的次数进行了统计，按男、女分为两组，再将每组柜员员工的月“不满意”次数分为5组：
，
，
，
，
，得到如下频数分布表．
分组 |
|
|
|
|
|
女柜员 | 2 | 3 | 8 | 5 | 2 |
男柜员 | 1 | 3 | 9 | 4 | 3 |
（1）在答题卡所给的坐标系中分别画出男、女柜员员工的频率分布直方图；分别求出男、女柜员员工的月平均“不满意”次数的估计值，试根据估计值比较男、女柜员员工的满意度谁高？
（2）在抽取的40名柜员员工中：从“不满意”次数不少于20的员工中随机抽取3人，并用X表示随机抽取的3人中女柜员工的人数，求X的分布列和数学期望．
【答案】（1）直方图见解析；男、女柜员月平均“不满意”次数的估计值分别为
，
；女柜员员工的满意度高；（2）分布列见解析，
【解析】
（1）分别列出女柜员、男柜员的频率分布表，再画出女柜员、男柜员的频率分布直方图；计算女柜员、男柜员员工的月平均“不满意”次数，比较即可得出结论．
（2）在抽取的40名柜员员工中，“不满意”次数不少于20的柜员员工共有5人，其中女员工2人，男员工3人，从“不满意”次数不少于20的柜员员工中随机抽取3人，故X的所有可能取值为0，1，2，分别写出分布列，求出数学期望值．
（1）对于女柜员列出频率分布表如下，
分组 | [0，5） | [5，10） | [10，15） | [15，20） | [20，25] |
女柜员 | 2 | 3 | 8 | 5 | 2 |
频率 | 0.1 | 0.15 | 0.4 | 0.25 | .0.1 |
对于男柜员列出频率分布表如下；
分组 | [0，5） | [5，10） | [10，15） | [15，20） | [20，25] |
男柜员 | 1 | 3 | 9 | 4 | 3 |
男柜员 | 0.05 | 0.15 | 0.45 | 0.2 | 0.15 |
分别求出每组的频率，画出的直方图如图．
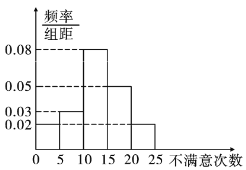女柜员
男柜员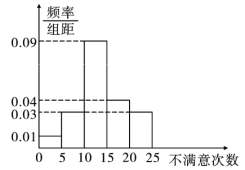 
设女、男柜员员工的月平均“不满意”次数分别为
，
，
则
，
，
，所以女柜员员工的满意度比男柜员员工的满意度要高．
（2）在抽取的40名柜员员工中，“不满意”次数不少于20的柜员员工共有5人，其中女员工2人，男员工3人，
从“不满意”次数不少于20的柜员员工中随机抽取3人，故X的所有可能取值为0，1，2，
则
，
，
，
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
所以
．
亮点激活精编提优100分大试卷系列答案
智趣寒假作业云南科技出版社系列答案
