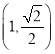题目内容
【题目】函数![]() ,当
,当![]() 时,
时,![]() 恒成立,则
恒成立,则![]() 的最大值是_____.
的最大值是_____.
【答案】![]()
【解析】
先根据恒成立写出有关a,b的约束条件,再在aob系中画出可行域,由斜率模型可得
![]() .又
.又![]() ,令
,令 ![]() t,则1≤t≤4,利用y=t
t,则1≤t≤4,利用y=t![]() 在[1,4]上单调递增,即可得出结论.
在[1,4]上单调递增,即可得出结论.
令g(m)=(3a﹣2)m+b﹣a.
由题意当m∈[0,1]时,0≤f(a)≤1可得
0≤g(0)≤1,
0≤g(1)≤1,
∴0≤b﹣a≤1,0≤2a+b﹣2≤1.
即 a≤b≤1+a①,2≤2a+b≤3 ②.
把(a,b)看作点画出可行域,由斜率模型![]() 可看作是原点与(a,b)连线的斜率,由图可得当(a,b)取点A时,原点与(a,b)连线的斜率最大,与b﹣a=0重合时原点与(a,b)连线的斜率最小.
可看作是原点与(a,b)连线的斜率,由图可得当(a,b)取点A时,原点与(a,b)连线的斜率最大,与b﹣a=0重合时原点与(a,b)连线的斜率最小.
∴1![]() 4.
4.
又 ![]() ,令
,令 ![]() t,则1≤t≤4,
t,则1≤t≤4,
∵y=t![]() 在[1,4]上单调递增,
在[1,4]上单调递增,
∴t=4时,即a![]() ,b
,b![]() 时,y有最大值是
时,y有最大值是![]() .
.
则![]() 的最大值是
的最大值是![]()
故答案为: ![]()
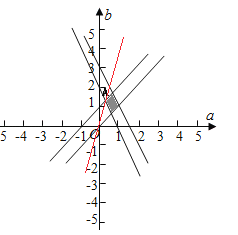

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目