题目内容
【题目】在如图所示的几何体中,四边形ABCD为正方形,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() .
.
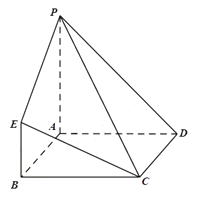
(1)求证:![]() 平面PAD;
平面PAD;
(2)在棱AB上是否存在一点F,使得平面![]() 平面PCE?如果存在,求
平面PCE?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】(1)证明见解析(2)存在,![]()
【解析】
(1)根据已知条件便可证明平面BCE∥平面PAD,从而便得到CE∥平面PAD;
(2)首先分别以AB,AD,AP三直线为x,y,z轴,建立空间直角坐标系,要使平面DEF⊥平面PCE,则有这两平面的法向量垂直,设![]() ,平面PCE的法向量为
,平面PCE的法向量为![]() ,根据
,根据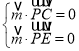 即可求出
即可求出![]() ,同样的办法表示出平面DEF的法向量
,同样的办法表示出平面DEF的法向量![]() ,根据
,根据![]() 即可求出
即可求出![]() ,从而求出
,从而求出![]() 的值.
的值.
解:(1)设PA中点为G,连结EG,DG,
因为![]() ,且
,且![]() ,
,![]() ,所以
,所以![]() 且
且![]() ,
,
所以四边形BEGA为平行四边形,所以![]() ,且
,且![]() .
.
因为正方形ABCD,所以![]() ,
,![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四边形CDGE为平行四边形,所以![]() .
.
因为![]() 平面PAD,
平面PAD,![]() 平面PAD,所以
平面PAD,所以![]() 平面PAD.
平面PAD.
(2)如图,建立空间坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
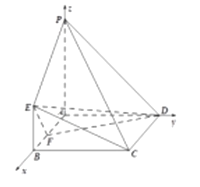
所以![]() ,
,![]() ,
,![]() .
.
设平面PCE的一个法向量为![]() ,
,
所以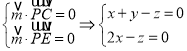
令![]() ,则,所以
,则,所以![]() .
.
假设存在点![]() 满足题意,则
满足题意,则![]() ,
,![]() .
.
设平面DEF的一个法向量为![]() ,
,
则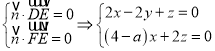 ,
,
令![]() ,则
,则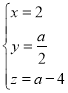 ,所以
,所以![]() .
.
因为平面![]() 平面PCE,所以
平面PCE,所以![]() ,即
,即![]() ,
,
所以![]() ,故存在点
,故存在点![]() 满足题意,且
满足题意,且![]() .
.

练习册系列答案
相关题目
【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率;
(2)根据统计数据估计图书分类错误的概率.
