Question

【题目】（本小题满分12分）已知圆C过点P（1，1），且与圆M：关于直线对称．

（1）求圆C的方程：

（2）设Q为圆C上的一个动点，求最小值；

（3）过点P作两条相异直线分别与圆C交与A，B，且直线ＰＡ和直线ＰＢ的倾斜角互补，Ｏ为坐标原点，试判断直线ＯＰ与直线ＡＢ是否平行？请说明理由．

Answer 1

【答案】（1）；（2）－4；（3）平行．

【解析】

试题（1）由题意圆心与圆心关于直线对称；（2）设，由（1）有，，可设，代入可求得的最小值；（3）本题证明用解析法，由于直线ＰＡ和直线ＰＢ的倾斜角互补，设方程为，则方程为，把它们代入圆的方程求得的坐标，计算得，即．

试题解析：（1）设圆心C（a,b），则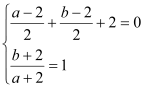 解得 a=0 b=0

所以圆C的方程为 ， 将点P的坐标代人得， 所以圆C的方程为．

（2）设Q（x,y） ，则

所以

所以的最小值为 -4 （可由线性规划或三角代换求得）

（3）由题意可知，直线ＰＡ和直线ＰＢ的斜率存在且互为相反数

故 可设ＰＡ： ＰＢ：

由 得

因为点P的横坐标是 x=1,一定是方程的解 故可得

同理

所以

所以直线ＯＰ与直线ＡＢ一定平行．