题目内容
9.a>0,a≠1,y=logax在[2,3]上的最大值比最小值大1,求a.分析 利用对数函数的单调性列出关系式,求解即可.
解答 解:当a>1时,由题意可得loga3-loga2=1,
解得a=$\frac{3}{2}$;
当0<a<1时,由题意可得loga2-loga3=1,
解得a=$\frac{2}{3}$.
综上a=$\frac{3}{2}或\frac{2}{3}$.
点评 本题考查对数函数的单调性与最值的求法,考查计算能力.

练习册系列答案
相关题目
19.已知定义在正整数集上的函数f(x)满足以下条件:①f(m+n)=f(m)+f(n)+mn,其中m,n为正整数;②f(3)=6.则f(100)=( )
| A. | 100 | B. | 4950 | C. | 5050 | D. | 5151 |
17.若a>0,b>0,ab+a-b=2$\sqrt{2}$,则ab-a-b的值为( )
| A. | $\sqrt{6}$ | B. | 2或-2 | C. | -2 | D. | 2 |
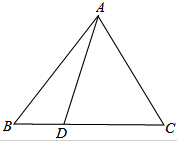 如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.
如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.