题目内容
19.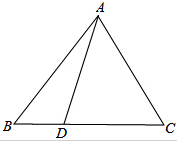 如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.
如图,△ABC中,|AB|=|AC|,D是BC边上任意一点,(D与B、C不重合),求证:|AB|2=|AD|2+|BD|•|DC|.
分析 由题意建立平面直角坐标系,设出所用点的坐标,得到向量的坐标,由向量的模证明答案.
解答 证明:建立如图所示直角坐标系,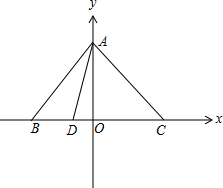
∵|AB|=|AC|,∴可设C(a,0),B(-a,0),
再设A(0,b)D(m,0),则$\overrightarrow{AB}=(-a,-b),\overrightarrow{AD}=(m,-b)$,
$\overrightarrow{BD}=(m+a,0),\overrightarrow{DC}=(a-m,0)$.
∴:|AB|2=$|\overrightarrow{AB}{|}^{2}={a}^{2}+{b}^{2}$,
|AD|2+|BD|•|DC|=$|\overrightarrow{AD}{|}^{2}+|\overrightarrow{BD}|•|\overrightarrow{DC}|$=m2+b2+(m+a)(a-m)=a2+b2,
∴|AB|2=|AD|2+|BD|•|DC|.
点评 本题考查平面向量的数量积运算,建立平面直角坐标系能够简化该题的证明过程,是中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
8.若有关x的方程x2lnx=kx-1有实数解,则实数k的取值范围为( )
| A. | (-∞,-1]∪[1,+∞) | B. | (-∞,-1] | C. | [1,+∞) | D. | (-∞,-1]∪(1,+∞) |