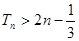题目内容
(本题满分12分)数列 的前
的前 项的和为
项的和为 ,对于任意的自然数
,对于任意的自然数 ,
,
(Ⅰ)求证:数列 是等差数列,并求通项公式
是等差数列,并求通项公式
(Ⅱ)设 ,求和
,求和
 的前
的前 项的和为
项的和为 ,对于任意的自然数
,对于任意的自然数 ,
,
(Ⅰ)求证:数列
 是等差数列,并求通项公式
是等差数列,并求通项公式(Ⅱ)设
 ,求和
,求和
(1)根据前n项和与通项公式的关系,结合定义法证明,并求解。
(2)而第二问关键是结合其通项公式,选择错位相减法来求和。
(2)而第二问关键是结合其通项公式,选择错位相减法来求和。
试题分析:解 :(1)令
 1分
1分 (2) (1)
(2) (1) 
 3分
3分 
 是等差数列 5分
是等差数列 5分  6分
6分 (2)

 ① 8分
① 8分  ②
② 10分
10分所以
 12分
12分点评:解决的关键是利用等差数列的通项公式和错位相减法来准确的求解运算,属于基础题。

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 }中,
}中, ,则
,则 ( )
( ) 中,
中, ,
, ,
, ,则该数列的通项为 。
,则该数列的通项为 。
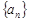 的前 n项和为
的前 n项和为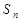 ,满足
,满足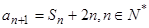 ,且
,且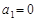 .
.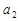 ,
,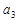 ;
; 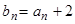 ,求证:数列
,求证:数列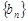 是等比数列。
是等比数列。 , 求数列
, 求数列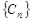 的前n项和
的前n项和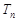 。
。 通项公式为
通项公式为 ,则
,则
 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为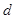 的等差数列;
的等差数列;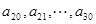 是公差为
是公差为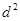 的等差数列(
的等差数列( ).
).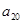 = 30,求
= 30,求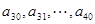 是公差为
是公差为 关于
关于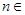 N
N );
); ,试用
,试用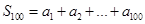
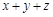 的值为 .
的值为 .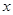
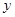
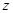
 }的通项公式为
}的通项公式为 达到最小时,n等于_________________.
达到最小时,n等于_________________.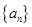 的前
的前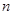 项和为
项和为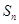 满足:
满足: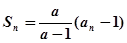 (
(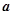 为常数,且
为常数,且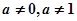 )
) 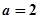 ,求数列
,求数列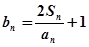 ,若数列
,若数列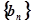 为等比数列,求
为等比数列,求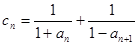 ,数列
,数列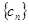 前
前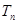 ,求证
,求证