题目内容
(本小题满分12分)
已知数列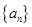 的前
的前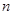 项和为
项和为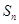 满足:
满足: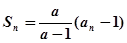 (
(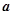 为常数,且
为常数,且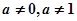 )
)
(1)若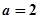 ,求数列
,求数列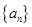 的通项公式
的通项公式
(2)设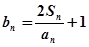 ,若数列
,若数列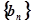 为等比数列,求
为等比数列,求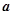 的值.
的值.
(3)在满足条件(2)的情形下,设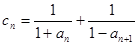 ,数列
,数列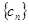 前
前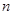 项和为
项和为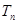 ,求证
,求证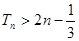
已知数列
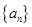 的前
的前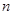 项和为
项和为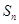 满足:
满足: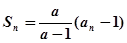 (
(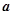 为常数,且
为常数,且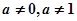 )
) (1)若
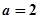 ,求数列
,求数列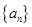 的通项公式
的通项公式(2)设
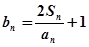 ,若数列
,若数列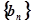 为等比数列,求
为等比数列,求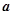 的值.
的值.(3)在满足条件(2)的情形下,设
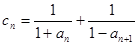 ,数列
,数列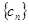 前
前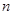 项和为
项和为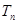 ,求证
,求证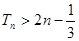
(1)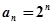 ;(2)
;(2)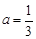 .(3)证明:由(2)知
.(3)证明:由(2)知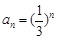 ,所以
,所以
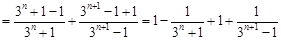
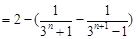 , 由
, 由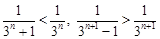 得
得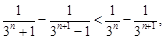
所以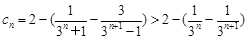 ,从而
,从而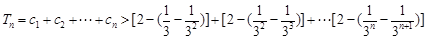
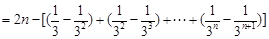
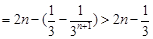 .
.
即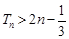 .
.
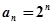 ;(2)
;(2)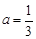 .(3)证明:由(2)知
.(3)证明:由(2)知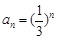 ,所以
,所以
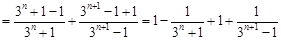
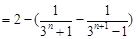 , 由
, 由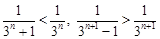 得
得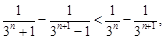
所以
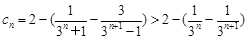 ,从而
,从而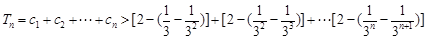
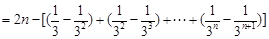
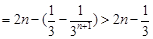 .
.即
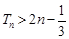 .
.试题分析:(1)当
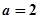 时,
时,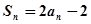
当
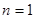 时,
时,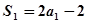
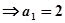
当
 时,
时,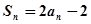
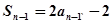
两式相减得到
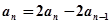 ,(
,(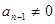 )得到
)得到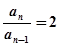
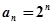
(2)由(Ⅰ)知,
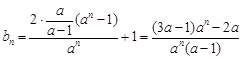 ,若
,若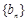 为等比数列,
为等比数列,则有
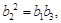 而
而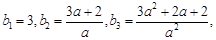
故
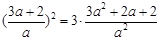 ,解得
,解得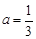 , 再将
, 再将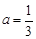 代入得
代入得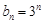 成立, 所以
成立, 所以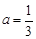 .
.(3)证明:由(2)知
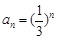 ,所以
,所以
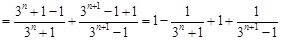
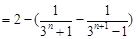 ,
, 由
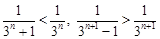 得
得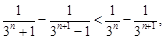
所以
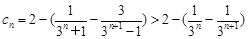 ,
, 从而
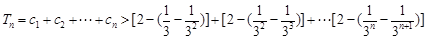
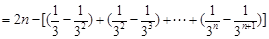
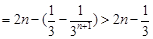 .
.即
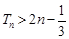 .
.点评:解决数列的前n项和的方法一般有:公式法、倒序相加法、错位相减法、分组求和法、裂项法等,要求学生掌握几种常见的裂项比如
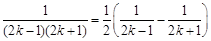

练习册系列答案
相关题目
 的前
的前 项的和为
项的和为 ,对于任意的自然数
,对于任意的自然数 ,
,
 ,求和
,求和
 是等差数列
是等差数列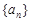 的前
的前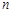 项和,若
项和,若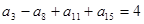 ,则
,则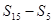 的值是
的值是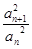 =p(p为正常数,n∈N+),则称{an}为“等方比数列”.
=p(p为正常数,n∈N+),则称{an}为“等方比数列”. 中,
中, ,
, .
. 是首项为
是首项为 ,公比为
,公比为 的等比数列,求
的等比数列,求 的前
的前 项和
项和 .
.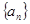 中,
中,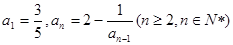 ,数列
,数列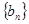 满足
满足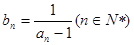 。
。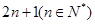 个正整数总和为
个正整数总和为 ,且这些数中后
,且这些数中后 个数的平方和与前
个数的平方和与前 .若
.若 ,则
,则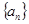 为单调递增的等差数列,
为单调递增的等差数列,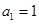 ,且
,且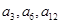 依次成等比数列.
依次成等比数列.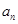 ;
; ,求数列
,求数列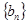 的前
的前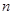 项和
项和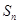 ;
;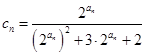 ,求数列
,求数列 的前
的前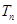 .
.