题目内容
2.已知函数f(x)=ex,g(x)=ln(x+1)(Ⅰ)讨论函数h(x)=f(x)-g(x)的单调性;
(Ⅱ)求证当x≥0时,f(x)g(x)≥x.
分析 (Ⅰ)先求出函数h(x)的导数,通过讨论h′(x)的情况,从而求出h(x)的单调性;
(Ⅱ)令p(x)=f(x)•g(x)-x,求出函数p(x)的导数,通过讨论p′(x)的情况,从而证出结论.
解答 解:(Ⅰ)易知h(x)的定义域为(-1,+∞),h′(x)=ex-$\frac{1}{x+1}$,
令φ(x)=ex-$\frac{1}{x+1}$,则φ′(x)=ex+$\frac{1}{{(x+1)}^{2}}$,
∵当x>-1时,φ′(x)>0,
∴函数φ(x)在区间(-1,+∞)上为增函数,
∴当-1<x≤0时,φ(x)≤φ(0)=0,即h′(x)≤0,
当x>0时,φ(x)>φ(0)=0,即h′(x)>0,
∴函数h(x)在区间(-1,0)上为减函数,在区间(0,+∞)上为增函数;
(Ⅱ)令p(x)=f(x)•g(x)-x,则p(x)=exln(x+1)-x,
p′(x)=exln(x+1)+$\frac{{e}^{x}}{x+1}$-1,
令s(x)=exln(x+1)+$\frac{{e}^{x}}{x+1}$-1,
则s′(x)=ex$[ln(x+1)+\frac{2x+1}{{(x+1)}^{2}}]$,
∴当x≥0时,ex>0,x+1≥1,
∴ln(x+1)≥0,$\frac{2x+1}{{(x+1)}^{2}}$>0,
∴s′(x)≥0,∴函数s(x)在区间(0,+∞)为增函数,
∴当x≥0时,s(x)≥s(0)=0,∴p′(x)≥0,
∴函数p(x)在区间[0,+∞)上是增函数,
∴当x≥0时,p(x)≥p(0)=0,
即当x≥0时,f(x)•g(x)≥x成立.
点评 本题考察了函数的单调性,考察导数的应用,求出函数的导数,讨论关于导函数的不等式是解答问题的关键,本题是一道中档题.

 如图所示,P、Q为△ABC内的两点,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,$\overrightarrow{AQ}$=$\frac{5}{3}$$\overrightarrow{AP}$-$\frac{1}{12}$$\overrightarrow{AC}$,则△ABP的面积与△ABQ的面积之比为( )
如图所示,P、Q为△ABC内的两点,且$\overrightarrow{AP}$=$\frac{2}{5}$$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$,$\overrightarrow{AQ}$=$\frac{5}{3}$$\overrightarrow{AP}$-$\frac{1}{12}$$\overrightarrow{AC}$,则△ABP的面积与△ABQ的面积之比为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{3}$ |
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
| A. | 焦点在x轴上的椭圆 | B. | 焦点在y轴上的椭圆 | ||
| C. | 焦点在x轴上的双曲线 | D. | 表示焦点在y轴上的双曲线 |
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{2}$ | D. | 2 |
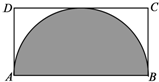 如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )
如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )