题目内容
已知函数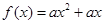 和
和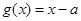 .其中
.其中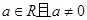 .
.
(1)若函数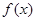 与
与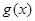 的图像的一个公共点恰好在
的图像的一个公共点恰好在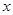 轴上,求
轴上,求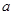 的值;
的值;
(2)若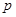 和
和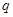 是方程
是方程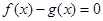 的两根,且满足
的两根,且满足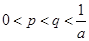 ,证明:当
,证明:当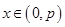 时,
时,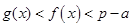 .
.
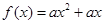 和
和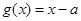 .其中
.其中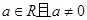 .
.(1)若函数
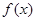 与
与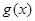 的图像的一个公共点恰好在
的图像的一个公共点恰好在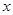 轴上,求
轴上,求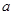 的值;
的值;(2)若
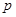 和
和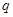 是方程
是方程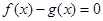 的两根,且满足
的两根,且满足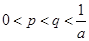 ,证明:当
,证明:当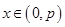 时,
时,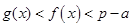 .
.(1)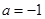 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
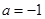 ;(2)证明过程详见解析.
;(2)证明过程详见解析.试题分析:本题考查一次函数与二次函数图像的关系以及作差法比较大小证明不等式问题,考查学生分析问题解决问题的能力.第一问,先求
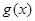 与
与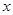 轴的交点,由已知得此交点同时也在
轴的交点,由已知得此交点同时也在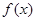 图像上,所以代入到
图像上,所以代入到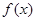 解析式中,解出
解析式中,解出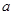 的值;第二问,作差法比较
的值;第二问,作差法比较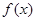 与
与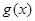 的大小,再用作差法比较
的大小,再用作差法比较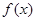 与
与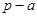 的大小.
的大小.试题解析:(1)设函数
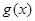 图象与
图象与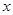 轴的交点坐标为
轴的交点坐标为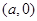 ,
,又∵点
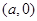 也在函数
也在函数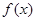 的图象上,∴
的图象上,∴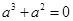 .
.而
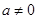 ,∴
,∴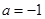 .(4分)
.(4分)(2)由题意可知
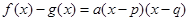 .
.∵
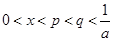 ,∴
,∴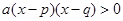 ,
,∴当
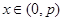 时,
时,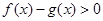 ,即
,即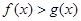 .(8分)
.(8分)又
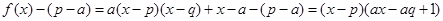 ,
,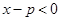 ,且
,且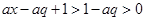 ,∴
,∴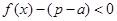 ,∴
,∴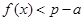 ,
,综上可知,
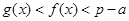 .(13分)
.(13分)
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
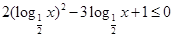 的解集为M,求当x∈M时函数
的解集为M,求当x∈M时函数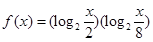 的最大、最小值.
的最大、最小值.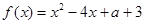 ,
,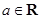 .
.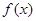 在
在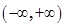 上至少有一个零点,求
上至少有一个零点,求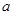 的取值范围;
的取值范围;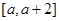 上的最大值为
上的最大值为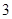 ,求
,求 ,满足
,满足 ,且
,且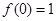 ,若在区间
,若在区间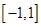 上,不等式
上,不等式 恒成立,则实数m的取值范围为 .
恒成立,则实数m的取值范围为 . (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 ,
,  、
、 的值;
的值; 在
在 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.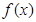 ,如果存在函数
,如果存在函数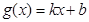 (k,b为常数),使得
(k,b为常数),使得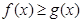 对一切实数x都成立,则称
对一切实数x都成立,则称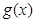 为函数
为函数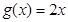 为函数
为函数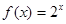 的一个承托函数.
的一个承托函数.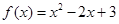 在区间
在区间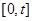 上有最大值3,最小值2,则
上有最大值3,最小值2,则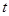 的取值范围是( )
的取值范围是( )


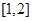
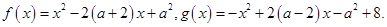 设
设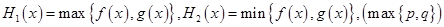 表示
表示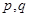 中的较大值,
中的较大值,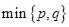 表示
表示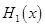 得最小值为
得最小值为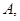
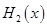 得最大值为
得最大值为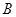 ,则
,则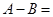 ( )
( )



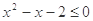 的整数解共有 个。
的整数解共有 个。