题目内容
已知函数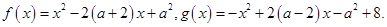 设
设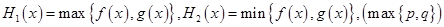 表示
表示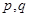 中的较大值,
中的较大值,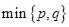 表示
表示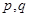 中的较小值,记
中的较小值,记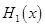 得最小值为
得最小值为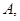
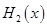 得最大值为
得最大值为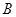 ,则
,则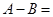 ( )
( )
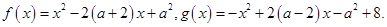 设
设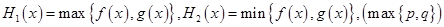 表示
表示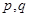 中的较大值,
中的较大值,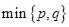 表示
表示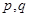 中的较小值,记
中的较小值,记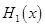 得最小值为
得最小值为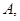
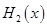 得最大值为
得最大值为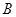 ,则
,则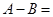 ( )
( )A. | B. | C. | D. |
C
试题分析:令h(x)=f(x)-g(x)=x2-2(a+2)x+a2-[-x2+2(a-2)x-a2+8]=2x2-4ax+2a2-8
=2(x-a)2-8.
① 由2(x-a)2-8=0,解得x=a±2,此时f(x)=g(x);
② 由h(x)>0,解得x>a+2,或x<a-2,此时f(x)>g(x);
③ 由h(x)<0,解得a-2<x<a+2,此时f(x)<g(x).
综上可知:(1)当x≤a-2时,则H1(x)=max{f(x),g(x)}=f(x)=[x-(a+2)]2-4a-2,
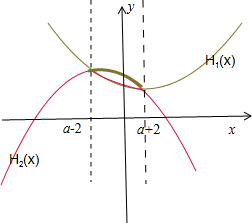
H2(x)=min{f(x),g(x)}=g(x)=-[x-(a-2)]2-4a+12,
(2)当a-2≤x≤a+2时,H1(x)=max{f(x),g(x)}=g(x),H2(x)
=min{f(x),g(x)}=f(x);
(3)当x≥a+2时,则H1(x)=max{f(x),g(x)}=f(x),
H2(x)=min{f(x),g(x)}=g(x),
故A=g(a+2)=-[(a+2)-(a-2)]2-4a+12=-4a-4,B=g(a-2)=-4a+12,
∴A-B=-4a-4-(-4a+12)=-16.
故选C.
点评:难题,作为一道选择题,是比较难的一道题目,关键是能根据二次函数的图象就行分析。

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 的图像顶点为
的图像顶点为 ,且图像在
,且图像在 轴截得的线段长为6.
轴截得的线段长为6. ;
; 在区间
在区间 上单调,求
上单调,求 的范围.
的范围.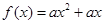 和
和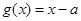 .其中
.其中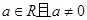 .
.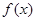 与
与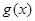 的图像的一个公共点恰好在
的图像的一个公共点恰好在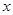 轴上,求
轴上,求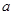 的值;
的值;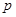 和
和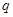 是方程
是方程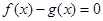 的两根,且满足
的两根,且满足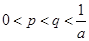 ,证明:当
,证明:当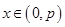 时,
时,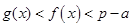 .
. x2-x+
x2-x+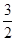 是[1,b]上的“四维光军”函数,求常数b的值;
是[1,b]上的“四维光军”函数,求常数b的值; 是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.
是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.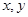 为实数,则
为实数,则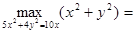 ___________
___________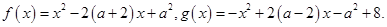 设
设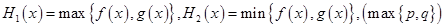 表示
表示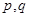 中的较大值,
中的较大值,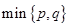 表示
表示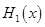 得最小值为
得最小值为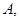
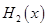 得最小值为
得最小值为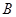 ,则
,则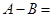




 ,函数
,函数 有最大值,则不等式
有最大值,则不等式 的解集为
的解集为  且关于
且关于 的方程
的方程 在
在 上有两个不相等的实数根.⑴求
上有两个不相等的实数根.⑴求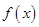 的解析式.⑵若
的解析式.⑵若 总有
总有 成立,求
成立,求 的最大值.
的最大值.