题目内容
【题目】已知椭圆![]() 的焦距为
的焦距为![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为椭圆
为椭圆![]() 上的两点(异于
上的两点(异于![]() ),连结
),连结![]() ,且
,且![]() 斜率是
斜率是![]() 斜率的
斜率的![]() 倍.
倍.
(1)求椭圆![]() 的方程;
的方程;
(2)证明:直线![]() 恒过定点.
恒过定点.
【答案】(1)![]() ;
;
(2)证明见解析.
【解析】
(1)根据题意列出方程组![]() ,解出方程组即可得椭圆方程;(2)连结
,解出方程组即可得椭圆方程;(2)连结![]() 设
设![]() ,由椭圆的性质可得出
,由椭圆的性质可得出![]() ,故而可得
,故而可得![]() ,当
,当![]() 斜率不存在时,设
斜率不存在时,设![]() ,解出
,解出![]() ,当直线斜率存在时,设
,当直线斜率存在时,设![]() ,联立直线与椭圆的方程,结合韦达定理,可得出
,联立直线与椭圆的方程,结合韦达定理,可得出![]() ,得出
,得出![]() 与
与![]() 的关系,代入直线方程即可得定点.
的关系,代入直线方程即可得定点.
(1)因为![]() ,所以
,所以![]() ,即椭圆
,即椭圆![]() 的方程为
的方程为![]()
(2)连结![]() 设
设![]() 则
则![]()
因为点![]() 在椭圆上,所以
在椭圆上,所以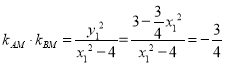
因为![]() ,所以
,所以![]()
当![]() 斜率不存在时,设
斜率不存在时,设![]() ,不妨设
,不妨设![]() 在
在![]() 轴上方,
轴上方,
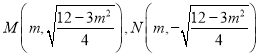
因为![]() ,所以
,所以![]()
(ii)当![]() 斜率存在时,设
斜率存在时,设![]() ,
,![]()
即![]() ,所以
,所以![]()
因为![]()
所以![]() ,即
,即![]() 或
或![]()
当![]() 时,
时,![]() ,恒过定点
,恒过定点![]() ,当斜率不存在亦符合:当
,当斜率不存在亦符合:当![]() ,
,![]() ,过点
,过点![]() 与点
与点![]() 重合,舍去.
重合,舍去.
所以直线恒过定点![]()

【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰坦尼克号》中一暮暮感人画面,让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济,更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型![]() 比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市
比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
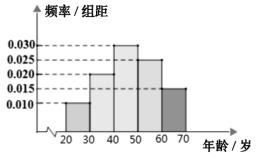
(1)求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄在
人,求所抽取的人中恰好没有年龄在![]() 段的概率.
段的概率.
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 30 | 45 |
很满意 | 25 | 10 | 35 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有99%的把握认为满意程度与年龄有关?
(2)为了帮助年龄在40岁以下的未购房的8名员工解决实际困难,该企业拟员工贡献积分![]() (单位:分)给予相应的住房补贴
(单位:分)给予相应的住房补贴![]() (单位:元),现有两种补贴方案,方案甲:
(单位:元),现有两种补贴方案,方案甲:![]() ;方案乙:
;方案乙: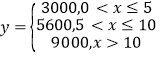 .已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“
.已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“![]() 类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“
类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“![]() 类员工”的概率。
类员工”的概率。
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |