题目内容
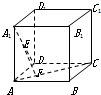 如图,在正方体ABCD-A1B1C1D1中,EF是异面直线AC与A1D的公垂线,则由正方体的八个顶点所连接的直线中,与EF平行的直线( )
如图,在正方体ABCD-A1B1C1D1中,EF是异面直线AC与A1D的公垂线,则由正方体的八个顶点所连接的直线中,与EF平行的直线( )分析:连结BD1、AD1,由线面垂直的判定与性质和正方体的性质,证出A1D⊥BD1且AC⊥BD1.根据题意EF是异面直线AC与A1D的公垂线,得到BD1∥EF.由于正方体的八个顶点所连接的直线中,除BD1外的其它直线与BD1都不平行,所以有且仅有一条直线BD1与EF平行.
解答:解: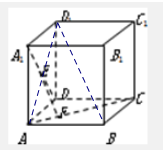 连结BD1、AD1,
连结BD1、AD1,
∵正方体ABCD-A1B1C1D1中,AB⊥平面AA1D1D,A1D?平面AA1D1D,
∴AB⊥A1D.
又∵正方形AA1D1D中,AD1⊥A1D,AB∩AD1=A,
∴A1D⊥平面ABD1,
∵BD1?平面ABD1,∴A1D⊥BD1
同理可得AC⊥BD1
∵EF是异面直线AC与A1D的公垂线,即AC⊥EF且A1D⊥EF,
∴BD1∥EF.
∵正方体的八个顶点所连接的直线中,除BD1外的其它直线与BD1都不平行,
∴有且仅有一条直线BD1与EF平行.
故选:A
 连结BD1、AD1,
连结BD1、AD1,∵正方体ABCD-A1B1C1D1中,AB⊥平面AA1D1D,A1D?平面AA1D1D,
∴AB⊥A1D.
又∵正方形AA1D1D中,AD1⊥A1D,AB∩AD1=A,
∴A1D⊥平面ABD1,
∵BD1?平面ABD1,∴A1D⊥BD1
同理可得AC⊥BD1
∵EF是异面直线AC与A1D的公垂线,即AC⊥EF且A1D⊥EF,
∴BD1∥EF.
∵正方体的八个顶点所连接的直线中,除BD1外的其它直线与BD1都不平行,
∴有且仅有一条直线BD1与EF平行.
故选:A
点评:本题给出正方体面对角的公垂线,判断正方体的八个顶点所连接的直线与此公垂线的位置关系.着重考查了线面垂直的判定与性质、空间直线的位置关系及其判定等知识,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )