题目内容
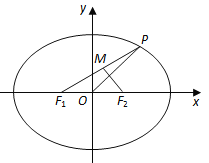
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
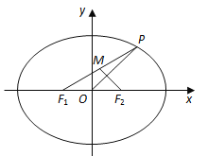
(1)若![]() ,点
,点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)若点![]() 横坐标为
横坐标为![]() ,点
,点![]() 为
为![]() 中点,且
中点,且![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意![]() ,然后将
,然后将![]() 点坐标代入方程,可求解出a,可得椭圆方程;
点坐标代入方程,可求解出a,可得椭圆方程;
(2)将P点横坐标代入椭圆方程可得P的坐标,可得![]() 的中点M的坐标,再由
的中点M的坐标,再由![]() ,可得a,c的关系式,从而求解离心率.
,可得a,c的关系式,从而求解离心率.
解:(1)设椭圆![]() 焦距为
焦距为![]() ,则
,则![]() ,
,
所以![]() .①
.①
又点![]()
![]() 在椭圆
在椭圆![]() :
:![]() 上,所以
上,所以![]() .②
.②
联立①②解得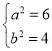 或
或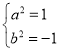 (舍去).
(舍去).
所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)设椭圆![]() 焦距为
焦距为![]() ,则
,则![]() ,
,![]() ,
,
![]() 代入
代入![]() 得
得![]() ,
,
不妨设点![]() 在
在![]() 轴上方,故点
轴上方,故点![]() 坐标为
坐标为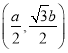 ,
,
又点![]() 为
为![]() 中点,故点
中点,故点![]() 坐标为
坐标为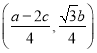 ,
,
所以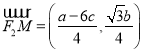 ,
,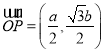 ,
,
由![]() 得
得![]() ,
,
即![]() ,化简得
,化简得![]() ,
,
将![]() 代入得
代入得![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,
,
因为![]() ,所以椭圆
,所以椭圆![]() 的离心率为
的离心率为![]() .
.

练习册系列答案
相关题目