题目内容
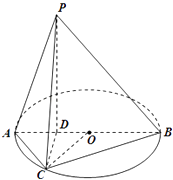
【题目】如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD= ![]() DB,点C为圆O上一点,且BC=
DB,点C为圆O上一点,且BC= ![]() AC.点P在圆O所在平面上的正投影为点D,PD=DB.
AC.点P在圆O所在平面上的正投影为点D,PD=DB. 
(1)求证:PA⊥CD;
(2)求二面角C﹣PB﹣A的余弦值.
【答案】
(1)证明:连接OC,由AD= ![]() BD知,点D为AO的中点,
BD知,点D为AO的中点,
又∵AB为圆的直径,∴AC⊥BC,
∵ ![]() AC=BC,∴∠CAB=60°,
AC=BC,∴∠CAB=60°,
∴△ACO为等边三角形,∴CD⊥AO.
∵点P在圆O所在平面上的正投影为点D,
∴PD⊥平面ABC,又CD平面ABC,
∴PD⊥CD,PD∩AO=D,
∴CD⊥平面PAB,PA平面PAB,
∴PA⊥CD.
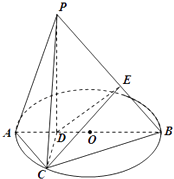
(2)解:过点D作DE⊥PB,垂足为E,连接CE,
由(1)知CD⊥平面PAB,又PB平面PAB,
∴CD⊥PB,又DE∩CD=D,
∴PB⊥平面CDE,又CE平面CDE,
∴CE⊥PB,
∴∠DEC为二面角C﹣PB﹣A的平面角.
由(1)可知CD= ![]() ,PD=BD=3,
,PD=BD=3,
∴PB=3 ![]() ,则DE=
,则DE= ![]() =
= ![]() ,
,
∴在Rt△CDE中,tan∠DEC= ![]() =
= ![]() ,
,
∴cos∠DEC= ![]() ,即二面角C﹣PB﹣A的余弦值为
,即二面角C﹣PB﹣A的余弦值为 ![]()
【解析】(1)先利用平面几何知识与线面垂直的性质证线线垂直,由线线垂直线面垂直,再由线面垂直线线垂直;(2)通过作出二面角的平面角,证明符合定义,再在三角形中求解.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).

 阅读快车系列答案
阅读快车系列答案【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。
