题目内容
【题目】已知双曲线![]() :
: ![]() .
.
(1)已知直线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)过点![]() 作直线
作直线![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,若弦
,若弦![]() 恰被点
恰被点![]() 平分,求直线
平分,求直线![]() 的方程.
的方程.
【答案】(1) m=±2 (2) 4x﹣y﹣2=0
【解析】试题分析:(Ⅰ)分别设A,B的坐标为(x1,y1),(x2,y2),根据弦长公式即可求出,
(Ⅱ)分别设M,N的坐标为(x3,y3),(x4,y4),可得y32﹣![]() x32=1,y42﹣
x32=1,y42﹣![]() x42=1,两式相减,再由中点坐标公式和直线的斜率公式,化简整理可得MN的斜率,再由点斜式方程可得所求直线方程
x42=1,两式相减,再由中点坐标公式和直线的斜率公式,化简整理可得MN的斜率,再由点斜式方程可得所求直线方程
试题解析:
解:(Ⅰ)分别设A,B的坐标为(x1,y1),(x2,y2)
由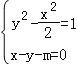 ,消y可得,x2﹣4mx+2(m2﹣1)=0,
,消y可得,x2﹣4mx+2(m2﹣1)=0,
∴x1+x2=4m,x1x2=2(m2﹣1),
∴|x1﹣x2|2=(x1+x2)2﹣4x1x2=16m2﹣8(m2﹣1)=8(m2+1),
∴|AB|=![]()
![]() =4
=4![]() ,解得m=±2,
,解得m=±2,
(Ⅱ)分别设M,N的坐标为(x3,y3),(x4,y4),可得y32﹣![]() x32=1,y42﹣
x32=1,y42﹣![]() x42=1,
x42=1,
两式相减,可得(y3﹣y4)(y3+y4)=![]() (x3﹣x4)(x3+x4),
(x3﹣x4)(x3+x4),
由点P(1,2)为MN的中点,
可得x3+x4=2,y3+y4=4,
∴4(y3﹣y4)=![]() ×2(x3﹣x4),∴kMN=
×2(x3﹣x4),∴kMN=![]() =4 经检验
=4 经检验![]()
即直线l的方程为y﹣2=4(x﹣1),即为4x﹣y﹣2=0

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目