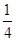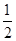题目内容
设函数f(x)在R上的导函数为f′(x),且2f(x)+xf′(x)>x2,下面不等式在R上恒成立的是( )
| A.f(x)>0 | B.f(x)<0 |
| C.f(x)>x | D.f(x)<x |
A
解析

练习册系列答案
相关题目
设函数 ,则
,则 ( )
( )
A.最大值为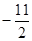 | B.最大值为 |
C.最小值为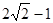 | D.最小值为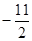 |
已知函数 的导函数为
的导函数为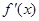 ,且满足关系式
,且满足关系式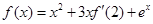 ,则
,则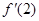 的值等于( )
的值等于( )
A.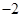 | B.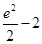 | C.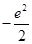 | D.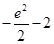 |
一物体的运动方程为s=3+t2,则在时间段[2,2.1]内相应的平均速度为( ).
| A.4.11 | B.4.01 |
| C.4.0 | D.4.1 |
设a∈R,若函数y=ex+ax,x∈R有大于零的极值点,则( )
| A.a<-1 | B.a>-1 |
C.a>- | D.a<- |
若存在过点(1,0)的直线与曲线y=x3和y=ax2+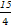 x-9都相切,则a等于( )
x-9都相切,则a等于( )
A.-1或-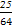 | B.-1或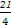 |
C.- 或- 或-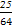 | D.- 或7 或7 |
已知f(x)是定义域为R的奇函数,f(-4)=-1,f(x)的导函数f′(x)的图像如图X18-1所示.若两正数a,b满足f(a+2b)<1,则 的取值范围是( )
的取值范围是( )
A.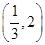 | B.(-∞,-1) | C.(-1,0) | D. |
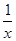 .
.