题目内容
(本小题满分16分)
公差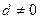 的等差数列
的等差数列 的前
的前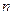 项和为
项和为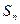 ,已知
,已知 ,
, .
.
(Ⅰ)求数列 的通项公式
的通项公式 及其前
及其前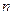 项和
项和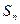 ;
;
(Ⅱ)记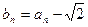 ,若自然数
,若自然数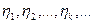 满足
满足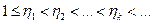 ,并且
,并且
 成等比数列,其中
成等比数列,其中 ,求
,求 (用
(用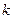 表示);
表示);
(Ⅲ)记 ,试问:在数列
,试问:在数列 中是否存在三
中是否存在三 项
项
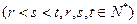 恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
公差
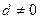 的等差数列
的等差数列 的前
的前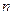 项和为
项和为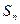 ,已知
,已知 ,
, .
.(Ⅰ)求数列
 的通项公式
的通项公式 及其前
及其前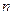 项和
项和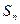 ;
;(Ⅱ)记
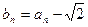 ,若自然数
,若自然数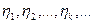 满足
满足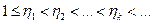 ,并且
,并且 成等比数列,其中
成等比数列,其中 ,求
,求 (用
(用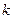 表示);
表示);(Ⅲ)记
 ,试问:在数列
,试问:在数列 中是否存在三
中是否存在三 项
项
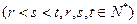 恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.(Ⅰ) ,
,
(Ⅱ)
(Ⅲ)不存在满足题 意的三项
意的三项 ,理由略
,理由略
 ,
,(Ⅱ)

(Ⅲ)不存在满足题
 意的三项
意的三项 ,理由略
,理由略解:(I) …………2分
…………2分
所以 ………………5分
………………5分
(II)由题意,
………………7分
 ………………10分
………………10分
(III)易知 成等比数列,
成等比数列,
则
即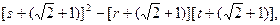
整理得 ………………12分
………………12分
①当 ,
,

②当 ,
,
从而 矛盾.
矛盾.
综上所述,不存在满足题 意的三项
意的三项 ………………16分
………………16分
 …………2分
…………2分所以
 ………………5分
………………5分(II)由题意,

………………7分
 ………………10分
………………10分(III)易知
 成等比数列,
成等比数列,则

即
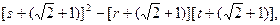
整理得
 ………………12分
………………12分①当
 ,
,
②当
 ,
,从而
 矛盾.
矛盾.综上所述,不存在满足题
 意的三项
意的三项 ………………16分
………………16分
练习册系列答案
相关题目
 12分)
12分) (
( ),比较
),比较 、
、 、
、 的大小,并证明你的结论
的大小,并证明你的结论 3分)
3分) 列
列 满足
满足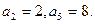
 的前n项和为Tn若
的前n项和为Tn若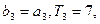 求Tn。
求Tn。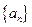 的首项
的首项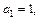 公差
公差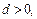 且第二项、第五项、第十四项分别是等比数列
且第二项、第五项、第十四项分别是等比数列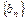 的第二项、第三项、第四项。
的第二项、第三项、第四项。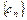 对任意正整数
对任意正整数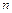 均有
均有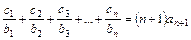 成立,
成立,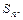
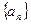 为等差数列,且
为等差数列,且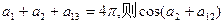 的值为 ( )
的值为 ( )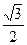 B
B .
.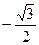 C.
C.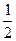 D.
D.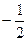
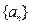 中,若
中,若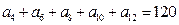 ,则
,则
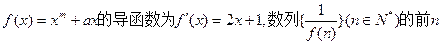 项和为
项和为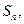 则
则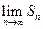 =" " ( )
=" " ( )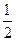
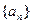 ,
,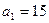 ,
,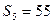 ,则过点
,则过点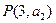 ,
,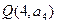 的直线的斜率为 ( )
的直线的斜率为 ( )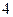
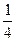
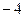
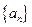 共有
共有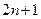 项,其中奇数项之和为319,偶数项
项,其中奇数项之和为319,偶数项 之和为290,则其中间项为 .
之和为290,则其中间项为 .