题目内容
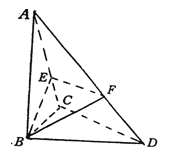
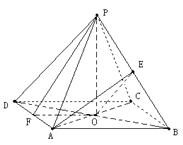
【题目】如图，在矩形
中， 
， 
，沿对角线
将
折起，使点
移到
点，且
在平面
上的射影
恰好落在
上.
（1）求证： 
；
（2）求点
到平面
的距离.
【答案】（1）见解析（2）
【解析】试题分析：（1）由折叠前后关系可得
,再由
得
，又
,由线面垂直判定定理得
,即得
,最后根据线面垂直判定定理得
（2）一般利用等体积法求点
到平面
的距离. 
可解得高即点
到平面
的距离.
试题解析：(1) 
, 
,
, 
, 
, 
, 
,又
, 
,
(2)方法1：由（1）知， 
，所以只需
， 
为所求距离，在
.
方法2：等体积法得， 
,
得
点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.线面角的寻找，主要找射影，即需从线面垂直出发确定射影，进而确定线面角.
练习册系列答案
相关题目
