题目内容
为了了解中学生的体能情况,抽取了某中学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如下图),已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4.第一小组的频数是5.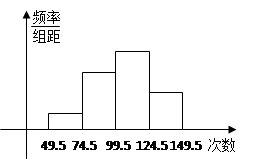
(1) 求第四小组的频率和参加这次测试的学生人数;
(2) 在这次测试中,学生跳绳次数的中位数落在第几小组内?
(3) 参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
(1) 0.2, 50人;(2)第三小组;(3) 60%.
解析试题分析:(1) 第四小组的频率=1-(0.1+0.3+0.4)=0.2,因为第一小组的频数为5,第一小组的频率为0.1,所以参加这次测试的学生人数为5¸0.1=50(人).
(2) 0.3´50=15,0.4´50=20,0.2´50=10,则第一、第二、第三、第四小组的频数分别为5,15,20,10.所以学生跳绳次数的中位数落在第三小组内.
(3) 跳绳成绩的优秀率为(0.4+0.2)´100%=60%.
考点:本题考查了频率分布直方图的运用
点评:频率分布直方图有以下特点:①频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率.直角坐标系中的纵轴表示频率与组距的比值,即小长方形面积=组距× =频率.②所有长方形面积的和等于1.③从频率分布直方图可以清楚地看出数据分布的总体态势,但是从直方图本身得不出原始的数据内容
=频率.②所有长方形面积的和等于1.③从频率分布直方图可以清楚地看出数据分布的总体态势,但是从直方图本身得不出原始的数据内容

通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如表所示:
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
(Ⅱ)根据上表提供的数据,用最小二乘法求线性回归直线方程=x+;
(Ⅲ)现投入资金10万元,估计获得的利润为多少万元?
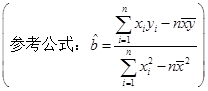
(10分)某种产品的广告费支出x与消费额y(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)预测当广告费支出为700万元时的销售额.
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式
 ,
, )
) (本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
| 甲 | 82 | 82 | 79 | 95 | 87 |
| 乙 | 95 | 75 | 80 | 90 | 85 |
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.


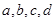 的值;
的值; 某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
 ,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区
,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区