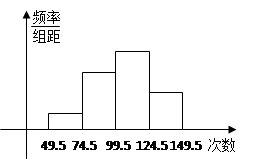题目内容
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成6组后,得到部分频率分布直方图(如图),观察图中的信息,回答下列问题.
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)根据频率分布直方图,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,记[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望。
(Ⅰ)0.3 (Ⅱ)71 (Ⅲ) X的分布列为:X 0 1 2 P 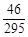
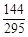
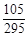
EX=0×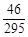 +1×
+1×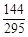 +2×
+2×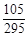 =
= .
.
解析试题分析:(Ⅰ)设分数在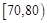 内的频率为x,根据频率分布直方图,
内的频率为x,根据频率分布直方图,
则有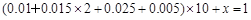 ,可得x="0.3."
,可得x="0.3."
所以频率分布直方图如图所示: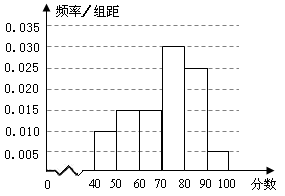
(Ⅱ)平均分为: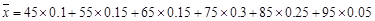
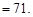
(Ⅲ)学生成绩在[40,70)的有0.4×60=24人,在[70,100]的有0.6×60=36人,
且X的可能取值是0,1,2.
则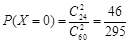 ,
,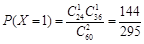 ,
,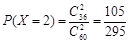 .
.
所以X的分布列为:X 0 1 2 P 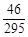
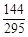
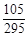
所以EX=0×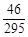 +1×
+1×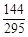 +2×
+2×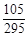 =
= .
.
考点:频率分布直方图;众数、中位数、平均数
点评:本题主要考查了频率及频率分布直方图,考查运用统计知识解决简单实际问题的能力,数据处理能力和运用意识,属于中档题.

某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 =bx+a;
=bx+a;(2)试预测加工10个零件需要多少时间?
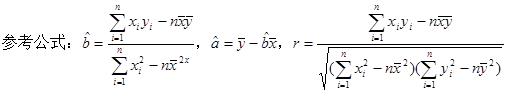
| n-2 | 1 | 2 | 3 | 4 |
| 小概率0.05 | 0.997 | 0.950 | 0.878 | 0.811 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 |
第 届亚运会于
届亚运会于 年
年 月
月 日至
日至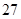 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了 名男志愿者和
名男志愿者和 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有 人和
人和 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下 列联表:
列联表:
| | 喜爱运动 | 不喜爱运动 | 总计 |
| 男 | 10 | | 16 |
| 女 | 6 | | 14 |
| 总计 | | | 30 |
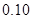 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?(3)如果从喜欢运动的女志愿者中(其中恰有
 人会外语),抽取
人会外语),抽取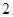 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中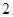 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?附:K2=
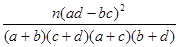
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如下图所示.
(Ⅰ)下表是年龄的频数分布表,求正整数a,b的值;
| 区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
| 人数 | 50 | 50 |  | 150 |  |
(III)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第三组 | (60,75] | 4 | 0.1 |
| 第四组 | (75,90) | 4 | 0.1 |
(Ⅱ)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(Ⅲ)将频率视为概率,对于去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为
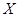 ,求
,求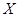 的分布列及数学期望
的分布列及数学期望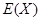 .
. (本题满分14分)
某零售店近五个月的销售额和利润额资料如下表:
| 商店名称 | A | B | C | D | E |
销售额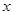 (千万元) (千万元) | 3 | 5 | 6 | 7 | 9 9 |
利润额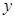 (百万元) (百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额
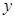 关于销售额
关于销售额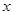 的回归直线方程;
的回归直线方程;(3)当销售额为4(千万元)时,利用(2)的结论估计该零售店的利润额(百万元).
 ,
,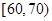 ,
,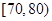 ,
,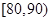 ,
, .
.
 的值;
的值; )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数( )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在 之外的人数.
之外的人数.