题目内容
(10分)某种产品的广告费支出x与消费额y(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)预测当广告费支出为700万元时的销售额.
(1)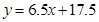 (2)63百万元
(2)63百万元
解析试题分析:(1)由表中数据可得: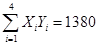 ,
,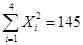 ,
, 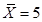 ,
,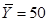 , …… 4分
, …… 4分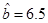 ;
;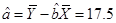 ,
,
所求的回归方程为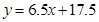 …… 7分
…… 7分
(2)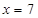 时,
时,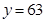
当广告费支出为700万元时的销售额为63百万元。 …… 10分
考点:本小题主要考查回归直线方程的求解与应用,考查学生的运算求解能力.
点评:当两变量具有线性相关关系时求出的回归直线方程才有意义.

练习册系列答案
相关题目
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了 至
至 月份每月
月份每月 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差 (°C) (°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 (个) (个) | 22 | 25 | 29 | 26 | 16 | 12 |
 组,用剩下的
组,用剩下的 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的 组数据进行检验.
组数据进行检验.(Ⅰ)求选取的
 组数据恰好是相邻两个月的概率;
组数据恰好是相邻两个月的概率;(Ⅱ)若选取的是
 月与
月与 月的两组数据,请根据
月的两组数据,请根据 至
至 月份的数据,求出
月份的数据,求出 关于
关于 的线性回归方程
的线性回归方程 ;(其中
;(其中 )
)(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过
 人,则认为得到的线性回归方程是理想的.试问该小组所得线性回归方程是否理想?
人,则认为得到的线性回归方程是理想的.试问该小组所得线性回归方程是否理想? (本小题满分12分)
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第三组 | (60,75] | 4 | 0.1 |
| 第四组 | (75,90) | 4 | 0.1 |
(2)求该样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由;
(3)将频率视为概率,对于去年的某2天,记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为
 ,求
,求 的分布列及数学期望
的分布列及数学期望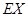 .
. 甲、乙两人在相同条件下各射击10次,每次命中的环数如下:
| 甲 | 8 | 6 | 7 | 8 | 6 | 5 | 9 | 10 | 4 | 7 |
| 乙 | 6 | 7 | 7 | 8 | 6 | 7 | 8 | 7 | 9 | 5 |
(1)分别计算以上两组数据的平均数;
(2)分别计算以上两组数据的方差;
公式:

(3)根据计算结果,估计一下两人的射击情况.

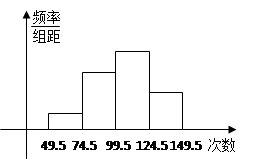
 ,
, ,…,
,…, 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
 的值;
的值; 与
与 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
 两所学校的学生体育锻炼严重不足的频率。
两所学校的学生体育锻炼严重不足的频率。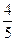 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为 ,
, (
( 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为



 。
。