题目内容
(本题满分10分)
在极坐标系中,已知两点O(0,0),B(2 ,
, ).
).
(1)求以OB为直径的圆C的极坐标方程,然后化成直角方程;
(2)以极点O为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(1)极坐标方程为:r=2 cos(q-
cos(q- ),直角方程为(x-2)2+(y-2)2=2
),直角方程为(x-2)2+(y-2)2=2
(2)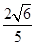
解析试题分析:(1)设P(r,q)为圆上任意一点,则|OP|=r,ÐPOx=q- ,
,
在RtDPOB中,cos(q- )=
)=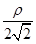 ,即r=2
,即r=2 cos(q-
cos(q- ).
).
∴r2=2 rcosq×
rcosq×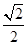 +2
+2 rsinq×
rsinq×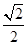 ,
,
∴圆C的直角坐标方程为 (x-2)2+(y-2)2=2. ……5分
(2)作CD^MN于D,C到直线l的距离为d=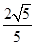 ,
,
在RtDCDA中,|MN|=2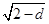 =
=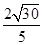 ,
,
∴S=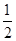 ×
×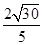 ×
×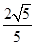 =
=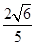 . ……10分
. ……10分
考点:本小题主要考查参数方程和直角方程的互化,直线与圆的位置关系,弦长的计算,和三角形面积公式的应用.
点评:当直线与圆相交时,要用到半径、半弦长和圆心到直线的距离构成一个直角三角形,利用勾股定理求解比较简单.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 与圆C:
与圆C: ,
, 相切,求m的值。
相切,求m的值。 ,求圆C 截直线L所得的弦长。
,求圆C 截直线L所得的弦长。 )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点. ,过原点
,过原点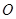 的直线
的直线 与圆
与圆 相交于
相交于 两点
两点 的长为
的长为 ,求直线
,求直线 为定值。
为定值。 、
、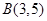 两点,且圆心C在直线
两点,且圆心C在直线 上.
上.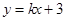 与⊙C总有公共点,求实数
与⊙C总有公共点,求实数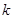 的取值范围.
的取值范围. .
. 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求 的取值范围.
的取值范围. |PD|.
|PD|.
 的圆形村落,
的圆形村落,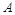 、
、 两人同时从村落中心出发。
两人同时从村落中心出发。 ,且后来
,且后来
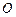 为平面直角坐标系的原点,过点
为平面直角坐标系的原点,过点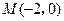 的直线
的直线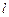 与圆
与圆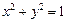 交于
交于 ,
,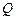 两点.
两点.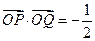 ,求直线
,求直线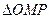 与
与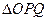 的面积相等,求直线
的面积相等,求直线