题目内容
(本题11分)已知圆 ,过原点
,过原点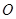 的直线
的直线 与圆
与圆 相交于
相交于 两点
两点
(1) 若弦 的长为
的长为 ,求直线
,求直线 的方程;
的方程;
(2)求证: 为定值。
为定值。
(1) ;(2)当
;(2)当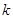 不存在时,直线为
不存在时,直线为 ,此时
,此时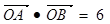 ,当
,当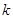 存在时,设直线
存在时,设直线 ,设
,设 ,
,
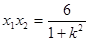 所以
所以 。
。
解析试题分析:(1)设直线方程 ,所以
,所以 ,………3分
,………3分
解得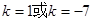
所以直线方程为 ……………………………5分
……………………………5分
(2)当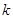 不存在时,直线为
不存在时,直线为 ,此时
,此时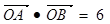 ……6分
……6分
当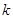 存在时,设直线
存在时,设直线 ,
,
设 ,
,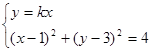 消y得
消y得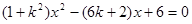 ,……7分
,……7分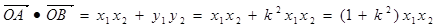
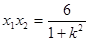 所以
所以
综上: ……………………………11分
……………………………11分
另法: 三点共线,
三点共线,
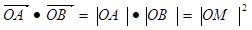 (
( =
=
考点:直线与圆的综合应用。
点评:在直线与圆相交时,我们通常用到弦心距、半径和弦长的一半构成的直角三角形来解题。属于基础题型。

练习册系列答案
相关题目
 截得的弦长是6.
截得的弦长是6. 的圆心为原点
的圆心为原点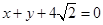 相切。
相切。
 (8,6)引圆O的两条切线
(8,6)引圆O的两条切线 ,切点为
,切点为 ,求直线
,求直线 的方程。
的方程。 :
: 交
交 轴于
轴于 两点,曲线
两点,曲线 是以
是以 为长轴,直线:
为长轴,直线: 为准线的椭圆.
为准线的椭圆.
 是直线上的任意一点,以
是直线上的任意一点,以 为直径的圆
为直径的圆 与圆
与圆 两点,求证:直线
两点,求证:直线 必过定点
必过定点 ,并求出点
,并求出点 两点,且
两点,且 ,试求此时弦
,试求此时弦 和点
和点 .
.
 向⊙
向⊙ 引切线
引切线 ,求直线
,求直线 截得的弦长为4的⊙
截得的弦长为4的⊙ 为(Ⅱ)中⊙
为(Ⅱ)中⊙ . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.  的圆心
的圆心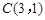 ,被
,被 轴截得的弦长为
轴截得的弦长为 .
. 交于
交于 ,
, 两点,且
两点,且 ,求
,求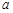 的值.
的值. ,
, ).
).
 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积. 是⊙
是⊙ 的直径,
的直径, 垂直于⊙
垂直于⊙ 是圆周上不同于
是圆周上不同于 的一动点.
的一动点.
 面PBC;
面PBC; ,则当直线
,则当直线 与平面
与平面 所成角正切值为
所成角正切值为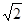 时,求直线
时,求直线 所成角的正弦值.
所成角的正弦值. 中,
中, 是抛物线
是抛物线
 的焦点,
的焦点, 是抛物线
是抛物线 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过 三点的圆的圆心为
三点的圆的圆心为 ,点
,点 .(Ⅰ)求抛物线
.(Ⅰ)求抛物线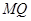 与抛物线
与抛物线 若存在,求出点
若存在,求出点