题目内容
12.已知函数y=f(x)是定义在R上的偶函数,且f(x+1)=f(x-1),当x∈[0,1]时,f(x)=2x-1,则函数g(x)=f(x)-lgx的零点个数为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 由f(x+1)=f(x-1),得f(x+2)=f(x),即函数y=f(x)的周期为2,作出函数y=f(x)和y=lgx的图象,利用数形结合法进行求解.
解答 解:∵f(x+1)=f(x-1),
∴f(x+2)=f(x),
即函数y=f(x)的周期为2,
当x∈[0,1]时,f(x)=2x-1,
若x∈[-1,0],则-x∈[0,1],
则f(-x)=2-x-1,
∵函数y=f(x)是定义在R上的偶函数,
∴f(-x)=2-x-1=f(x),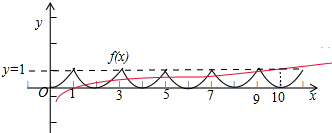
即f(x)=2-x-1,x∈[-1,0],
作出f(x)的图象如图,
由g(x)=f(x)-lgx=0,
则f(x)=lgx,
函数y=f(x)的周期为2,
当x>10时,y=lgx>1,此时函数y=lgx与f(x)无交点,
由图象可知两个图象的交点个数为9个,
即函数g(x)=f(x)-lgx的零点个数为9个,
故选:D.
点评 本题主要考查了周期函数与对数函数的图象,数形结合是高考中常用的方法,考查数形结合,本题属于中档题.

练习册系列答案
相关题目
2.不等式x2-2x-3<0成立的充要条件是( )
| A. | -1<x<3 | B. | 0<x<3 | C. | -2<x<3 | D. | -2<x<1 |
20.已知函数f(x)=$\left\{\begin{array}{l}{1-{e}^{-x},x≤0}\\{\sqrt{2x},x>0}\end{array}\right.$,若|f(x)|≥ax,则实数a的取值范围为( )
| A. | (-∞,0] | B. | (-∞,-1] | C. | [-2,0] | D. | [-1,0] |
7.设函数f(x)在R上存在导数f′(x),?x∈R,有f(-x)+f(x)=x2,在(0,+∞)上f′(x)<x,若f(6-m)-f(m)-18+6m≥0,则实数m的取值范围为( )
| A. | [-3,3] | B. | [3,+∞) | C. | [2,+∞) | D. | (-∞,-2]∪[2,+∞) |
17.己知集合M={x|-2<x<3},N={x|lgx≥0},则M∩N=( )
| A. | (-2,+∞) | B. | [1,3) | C. | (-2,-1] | D. | (-2,3) |