题目内容
4．函数y=x2-2x-3在x∈[-3，2]上的值域是[-4，12]．分析 先求出函数的对称轴，得到函数的单调区间，从而求出函数的值域即可．
解答 解：∵y=x2-2x-3=（x-1）2-4，
∴对称轴x=1，
∴函数在[-3，1）递减，在（1，2]递增，
∴x=1时：y最小，最小值是-4，
x=-3时：y最大，最大值是12，
故答案为：[-4，12]．
点评 本题考查了二次函数的性质，考查函数的单调性、值域问题，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．
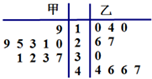从甲、乙两种玉米中各抽测了10株玉米苗的高度（单位：cm），其茎叶图如图所示，根据茎叶图，下列描述正确的是（ ）
从甲、乙两种玉米中各抽测了10株玉米苗的高度（单位：cm），其茎叶图如图所示，根据茎叶图，下列描述正确的是（ ）| A． | 甲种玉米苗的平均高度大于乙种玉米苗的高度，且甲种玉米苗比乙种玉米苗长得整齐 | |
| B． | 甲种玉米苗的平均高度大于乙种玉米苗的高度，但乙种玉米苗比甲种玉米苗长得整齐 | |
| C． | 乙种玉米苗的平均高度大于甲种玉米苗的高度，且乙种玉米苗比甲种玉米苗长得整齐 | |
| D． | 乙种玉米苗的平均高度大于甲种玉米苗的高度，但甲种玉米苗比乙种玉米苗长得整齐 |
在三棱锥S-ABC中，∠ASB=∠BSC=60°，∠ASC=90°，且SA=SB=SC，求证：平面ASC⊥平面ABC．