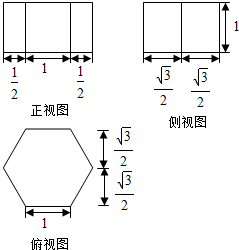
题目内容
12.已知cosθ=$\frac{5}{13}$,θ∈(π,2π),求sin($θ-\frac{π}{6}$),cos($θ-\frac{π}{6}$)及tan($θ-\frac{π}{6}$)的值.分析 由条件利用同角三角函数的基本关系求得sinθ、tanθ的值,再利用两角和差的三角公式求得sin($θ-\frac{π}{6}$),cos($θ-\frac{π}{6}$)及tan($θ-\frac{π}{6}$)的值.
解答 解:∵cosθ=$\frac{5}{13}$,θ∈(π,2π),∴sinθ=-$\sqrt{{1-cos}^{2}θ}$=-$\frac{12}{13}$,tanθ=$\frac{sinθ}{cosθ}$=-$\frac{12}{5}$,
∴sin($θ-\frac{π}{6}$)=sinθcos$\frac{π}{6}$-cosθsin$\frac{π}{6}$=-$\frac{12}{13}$•$\frac{\sqrt{3}}{2}$-$\frac{5}{13}$•$\frac{1}{2}$=-$\frac{12\sqrt{3}+5}{26}$,
cos($θ-\frac{π}{6}$)=cosθcos$\frac{π}{6}$+sinθsin$\frac{π}{6}$=$\frac{5}{13}•\frac{\sqrt{3}}{2}$-$\frac{12}{13}$•$\frac{1}{2}$=$\frac{5\sqrt{3}-12}{26}$,
tan($θ-\frac{π}{6}$)=$\frac{tanθ-tan\frac{π}{6}}{1+tanθ•tan\frac{π}{6}}$=$\frac{-\frac{12}{5}-\frac{\sqrt{3}}{3}}{1-\frac{12}{5}•\frac{\sqrt{3}}{3}}$=$\frac{-36-5\sqrt{3}}{15-12\sqrt{3}}$=$\frac{1476+612\sqrt{3}}{207}$=$\frac{164+68\sqrt{3}}{23}$.
点评 本题主要考查同角三角函数的基本关系,两角和差的三角公式,属于基础题.

| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
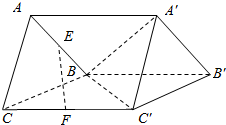 如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)