题目内容
14.设$\overrightarrow{a}$,$\overrightarrow{b}$为两个互相垂直的单位向量,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=m$\overrightarrow{a}$+n$\overrightarrow{b}$.若△ABC是以A为直角顶点的等腰直角三角形,则m+n=( )| A. | 1或-3 | B. | -1或3 | C. | 2或-4 | D. | -2或4 |
分析 根据△ABC是以A为直角顶点的等腰直角三角形可得出$\overrightarrow{AB}$和$\overrightarrow{AC}$的关系,用已知向量表示出$\overrightarrow{AB}$和$\overrightarrow{AC}$,列出关系式,即可求出答案.
解答 解:∵△ABC是等腰直角三角形,∠A为直角,
∴AB⊥AC,$\overrightarrow{AB}•\overrightarrow{AC}$=0;
由已知得,$\overrightarrow{AB}$=$\overrightarrow{OB}-\overrightarrow{OA}$=$\overrightarrow{b}-\overrightarrow{a}$;
$\overrightarrow{AC}$=$\overrightarrow{OC}-\overrightarrow{OA}$=(m-1)$\overrightarrow{a}$+n$\overrightarrow{b}$;
∴$\overrightarrow{AB}•\overrightarrow{AC}$=($\overrightarrow{b}-\overrightarrow{a}$)[(m-1)$\overrightarrow{a}$+n$\overrightarrow{b}$]=m-n-1=0;
即m-n=1;
又△ABC是等腰三角形,
∴AB=AC,$|\overrightarrow{AB}|$=$|\overrightarrow{AC}|$;
∵$|\overrightarrow{AB}|$=$\sqrt{{1}^{2}{+1}^{2}}=\sqrt{2}$,
∴$|\overrightarrow{AC}|$=$\sqrt{{(m-1)}^{2}{+n}^{2}}$=$\sqrt{2}$,得(m-1)2+n2=2;
∵m-n=1,
∴m=n+1,代入方程,得2n2=2,n=±1;
∴$\left\{\begin{array}{l}{n=1}\\{m=2}\end{array}\right.$或$\left\{\begin{array}{l}{n=-1}\\{m=0}\end{array}\right.$;
∴m+n=3或m+n=-1.
故答案选:B.
点评 本题考查了平面向量的基本定理,解题的关键是熟练掌握向量的运算法则.

 天天练口算系列答案
天天练口算系列答案| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
(Ⅰ)求该学校高一新生A、B两类学生各多少人?
(Ⅱ)经过测试,得到以下三个数据图表:
图一:75分以上A、B两类参加测试学生成绩的茎叶图(茎、叶分别是十位和个位上的数字)(如图1)
图二:100名测试学生成绩的频率分布直方图2;

表一:100名测试学生成绩频率分布表;
| 组号 | 分组 | 频数 | 频率 |
| 1 | [55,60) | 5 | 0.05 |
| 2 | [60,65) | 20 | 0.20 |
| 3 | [65,70) | ||
| 4 | [70,75) | 35 | 0.35 |
| 5 | [75,80) | ||
| 6 | [80,85) | ||
| 合计 | 100 | 1.00 | |
②该学校拟定从参加考试的79分以上(含79分)的B类学生中随机抽取2人代表学校参加市比赛,求抽到的2人分数都在80分以上的概率.
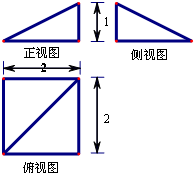
| A. | $\frac{9}{2}$πcm3 | B. | 36πcm3 | C. | $\frac{64}{3}$πcm3 | D. | 9πcm3 |
 在正三棱柱ABC-A1B1C1中,点D是BC的中点.
在正三棱柱ABC-A1B1C1中,点D是BC的中点.