题目内容
设函数 .
.
(1)若曲线 在点
在点 处与直线
处与直线 相切,求
相切,求 的值;
的值;
(2)求函数 的单调区间与极值点.
的单调区间与极值点.
(3)设函数 的导函数是
的导函数是 ,当
,当 时求证:对任意
时求证:对任意
 成立
成立
(1)a=4,b=24
(2)当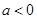 时,
时,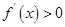 ,函数
,函数 在
在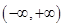 上单调递增,此时函数
上单调递增,此时函数 没有极值点
没有极值点
当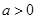 时,由
时,由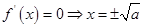 ,此时
,此时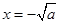 是
是 的极大值点,
的极大值点,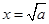 是
是 的极小值点.
的极小值点.
(3)根据由(2)知 在
在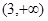 上单调递增,又
上单调递增,又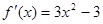 在
在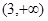 上也单调递增,函数单调性来证明不等式
上也单调递增,函数单调性来证明不等式
解析

练习册系列答案
相关题目
题目内容
设函数 .
.
(1)若曲线 在点
在点 处与直线
处与直线 相切,求
相切,求 的值;
的值;
(2)求函数 的单调区间与极值点.
的单调区间与极值点.
(3)设函数 的导函数是
的导函数是 ,当
,当 时求证:对任意
时求证:对任意
 成立
成立
(1)a=4,b=24
(2)当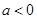 时,
时,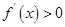 ,函数
,函数 在
在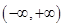 上单调递增,此时函数
上单调递增,此时函数 没有极值点
没有极值点
当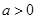 时,由
时,由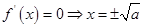 ,此时
,此时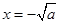 是
是 的极大值点,
的极大值点,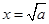 是
是 的极小值点.
的极小值点.
(3)根据由(2)知 在
在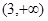 上单调递增,又
上单调递增,又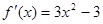 在
在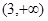 上也单调递增,函数单调性来证明不等式
上也单调递增,函数单调性来证明不等式
解析
