题目内容
【题目】中心在原点的椭圆C1与双曲线C2具有相同的焦点，F1（﹣c，0），F2（c，0），P为C1与C2在第一象限的交点，|PF1|=|F1F2|且|PF2|=5，若椭圆C1的离心率 
，则双曲线的离心率e2的范围是（ ）
A.
B.
C.（2，3）
D.
【答案】C
【解析】解：设椭圆的方程为 
+ 
=1（a＞b＞0）， 其离心率为e1 ，
双曲线的方程为 
﹣ 
=1（m＞0，n＞0），其离心率为e2 ，
|F1F2|=2c，
∵有公共焦点的椭圆与双曲线在第一象限的交点为P，
△PF1F2是以PF2为底边的等腰三角形，
∴在椭圆中，|PF1|+|PF2|=2a，而|PF1|=|F1F2|=2c，
∴|PF2|=2a﹣2c，①
同理，在该双曲线中，|PF2|=2c﹣2m；②
由①②可得m=2c﹣a．
∵e1= 
∈（ 
， 
），
∴ 
＜ 
＜ 
，
又e2= 
= 
= 
= 
∈（2，3）．
故选：C．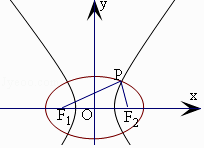
设椭圆的方程为 + =1（a＞b＞0）（a＞b＞0），其离心率e1 ， 双曲线的方程为 ﹣ =1（m＞0，n＞0），离心率为e2 ， 由e1= ∈（ ， ），e2= ，由△PF1F2是以PF2为底边的等腰三角形，结合椭圆与双曲线的定义可求得m=2c﹣a，从而可求得答案．
练习册系列答案
阅读快车系列答案
相关题目
