题目内容
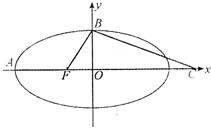
如图,F是椭圆
+
=1(a>b>0)的一个焦点,A、B是椭圆的两个顶点,椭圆的离心率为
,点C在x轴上,BC⊥BF,由B、C、F三点确定的圆M恰好与直线x+
y+3=0相切.
(I)求椭圆的方程;
(II)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点,若在x轴上存在一点N(x0,0),使得直线NP与直线NQ关于x轴对称,求x0的值.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
(I)求椭圆的方程;
(II)过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点,若在x轴上存在一点N(x0,0),使得直线NP与直线NQ关于x轴对称,求x0的值.

(I)由题意可知F(-c,0)
∵e=
,∴b=
c,即B(0,
c),∴kBF=
=
又∵BC⊥BF,∴kBC=-
,
∴C(3c,0),∴圆M的圆心坐标为(c,0),半径为2c由直线x+
y+3=0与圆M相切可得
=2c,
∴c=1,∴椭圆的方程为
+
=1.
(II)由题意可设直线l的方程为y=k(x+1)(k≠0),设P(x1,y1),Q(x2,y2)
∵直线NP与直线NQ关于x轴对称,
∴kNP=-kNQ,即
=-
∴
=-
,∴x0=
∵
,∴3x2+4k2(x+1)2=12
∴(3+4k2)x2+8k2x+4k2-12=0,
∴x1+x2=-
,x1x2=
,
∴x0=
=-4
∵e=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 0-(-c) |
| 3 |
又∵BC⊥BF,∴kBC=-
| ||
| 3 |
∴C(3c,0),∴圆M的圆心坐标为(c,0),半径为2c由直线x+
| 3 |
| |c+3| | ||||
|
∴c=1,∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)由题意可设直线l的方程为y=k(x+1)(k≠0),设P(x1,y1),Q(x2,y2)
∵直线NP与直线NQ关于x轴对称,
∴kNP=-kNQ,即
| y1 |
| x1-x0 |
| y2 |
| x2-x0 |
∴
| k(x1+1) |
| x1-x0 |
| k(x2+1) |
| x2-x0 |
| x1+x2+2x1x2 |
| x1+x2+2 |
∵
|
∴(3+4k2)x2+8k2x+4k2-12=0,
∴x1+x2=-
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∴x0=
-
| ||||
2-
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目