Question

【题目】设，满足约束条件.

（1）画出不等式表示的平面区域，并求该平面区域的面积；

（2）若目标函数的最大值为4，求的最小值.

Answer 1

【答案】(1) .

(2)4.

【解析】分析：（1）利用约束条件画出可行域，然后求解可行域面积即可；

（2）求出目标函数的最优解，得到a，b的关系式，然后利用基本不等式求解最小值即可.

详解：（1）不等式表示的平面区域如图所示阴影部分.

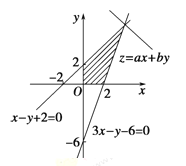
联立得点C坐标为(4,6)

平面区域的面积.

（2）当直线ax+by=z(a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点C(4,6)时,

目标函数z=ax+by(a>0,b>0)取得最大值4,即4a+6b=4,

即.

所以

等号成立当且仅当时取到.

故的最小值为4.