题目内容
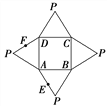
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】由题意画出四棱锥P-ABCD如图所示,

∵E,F分别为PA,PD的中点,
∴![]() ,且
,且![]() 。
。
∴![]() ,且
,且![]() 。
。
∴四边形EFCB为梯形,所以直线BE与直线CF相交。故①不正确。
结合图形可得直线BE与直线AF异面,故②正确。
由![]() ,
, ![]() 平面PBC,
平面PBC, ![]() 平面PBC,可得直线EF∥平面PBC。故③正确。
平面PBC,可得直线EF∥平面PBC。故③正确。

对于④,如图,假设平面BCEF⊥平面PAD。
过点P作PO⊥EF分别交EF、AD于点O、N,在BC上取一点M,连接PM、OM、MN,
∴PO⊥OM,
又PO=ON,
∴PM=MN。
若PM≠MN时,必然平面BCEF与平面PAD不垂直。故④不一定成立。
综上只有②③正确。选B。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目


