题目内容
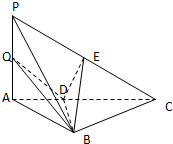
如图,在四棱锥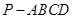 中,
中, ,
,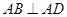 ,
,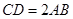 ,
, 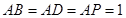 ,
,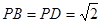 ,
, 和
和 分别是
分别是 和
和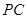 的中点.
的中点.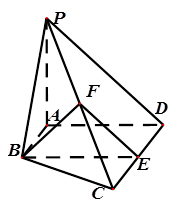
(1)求证:  底面
底面 ;
;
(2)求证:平面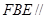 平面
平面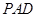 ;
;
(3)求三棱锥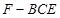 的体积.
的体积.
(1)关键是找出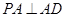 ,
, (2)关键是证明
(2)关键是证明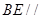 平面
平面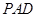 ,
, (3)
(3)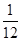
解析试题分析:(Ⅰ)证明:∵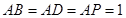 ,
,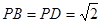 ,
, ,
,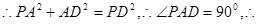
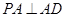 ,同理可得:
,同理可得: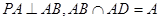
∴ 底面
底面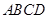
(Ⅱ)证明:∵ ,
,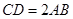 ,
,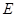 是
是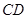 的中点,∴ABED为平行四边形
的中点,∴ABED为平行四边形
∴
又∵ 平面
平面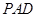 ,
,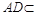 平面
平面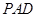 ,
,
∴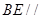 平面
平面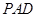 .
.
由于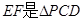 的中位线,
的中位线, 同理得
同理得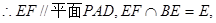
所以:平面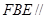 平面
平面
(Ⅲ)由(Ⅰ)知 底面
底面 ,
,
由已知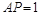 ,
, 是
是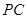 的中点,得
的中点,得 到底面
到底面 的距离为
的距离为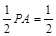 ,
,
由已知 ,
,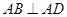 ,
,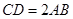 ,
,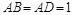 ,
,
∴三角形BCE的面积为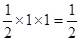 ,
,
∴三棱锥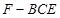 的体积为
的体积为 .
.
考点:直线与平面垂直的判定定理;直线与平面平行的判定定理;三棱锥的体积
点评:在立体几何中,常考的定理是:直线与平面垂直的判定定理、直线与平面平行的判定定理。当然,此类题目也经常要我们求出几何体的体积和表面积。

练习册系列答案
相关题目
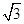 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.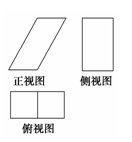
 ,在直角梯形
,在直角梯形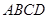 中,
中,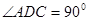 ,
,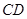 ∥
∥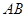 ,
, ,
,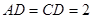 ,将
,将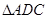 沿
沿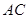 折起,使平面
折起,使平面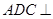 平面
平面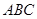 ,得到几何体
,得到几何体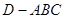 ,如图2所示.
,如图2所示.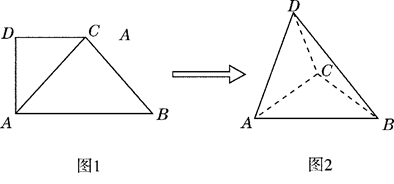
 平面
平面 ;
; 是边长为2的正方形,
是边长为2的正方形, ⊥平面
⊥平面 ,
, //
// 且
且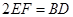 .
.
 ⊥平面
⊥平面 ;
; 的体积.
的体积.  在正视图中所示位置:
在正视图中所示位置: 为所在线段中点,
为所在线段中点, 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从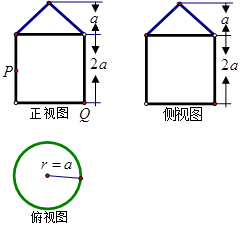

 中.
中.
 与
与 所成的角;
所成的角; ⊥平面
⊥平面 .
.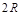 .
.