题目内容
如图, 是边长为2的正方形,
是边长为2的正方形, ⊥平面
⊥平面 ,
, ,
, //
// 且
且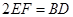 .
.
(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)求几何体 的体积.
的体积.
(Ⅰ)详见解析;(Ⅱ)2.
解析试题分析:(Ⅰ)利用垂直关系进行转化,最后借助面面垂直的判断定理证明平面 ⊥平面
⊥平面 ;(Ⅱ)采用体积分割的思路进行求解.即
;(Ⅱ)采用体积分割的思路进行求解.即 ,然后明确几何体的高进行求解.
,然后明确几何体的高进行求解.
试题解析:(Ⅰ)∵ ED⊥平面 ,AC
,AC 平面
平面 ,∴ ED⊥AC. 2分
,∴ ED⊥AC. 2分
∵  是正方形,∴ BD⊥AC, 4分
是正方形,∴ BD⊥AC, 4分
∴ AC⊥平面BDEF. 6分
又AC?平面EAC,故平面EAC⊥平面BDEF.
(Ⅱ)连结FO,∵ EF
 DO,∴ 四边形EFOD是平行四边形.
DO,∴ 四边形EFOD是平行四边形.
由ED⊥平面 可得ED⊥DO,
可得ED⊥DO,
∴ 四边形EFOD是矩形. 8分
方法一:∴ ∥
∥ ,
,
而ED⊥平面 ,∴
,∴  ⊥平面
⊥平面 .
.
∵  是边长为2的正方形,∴
是边长为2的正方形,∴ .
.
由(Ⅰ)知,点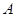 、
、 到平面BDEF的距离分别是
到平面BDEF的距离分别是 、
、 ,
,
从而 ;
;
方法二:∵ 平面EAC⊥平面BDEF.
∴ 点F到平面ACE的距离等于就是Rt△EFO斜边EO上的高,且高 . 10分
. 10分
∴几何体ABCDEF的体积
=
=2. 12分
考点:1.面面垂直的证明;2.几何体的体积.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 ),
),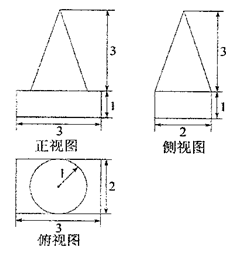
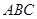 中,
中,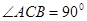 ,
,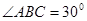 ,
,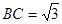 ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心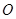 在边
在边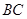 上,半圆与
上,半圆与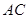 、
、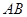 分别相切于点
分别相切于点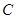 、
、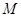 ,与
,与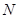 ),将△
),将△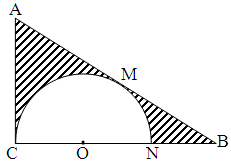
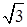 ,AD=CD=1.
,AD=CD=1.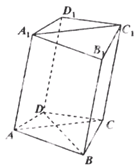
 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形 是菱形,且
是菱形,且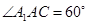 ,求四棱柱
,求四棱柱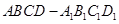 的体积.
的体积.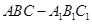 中,
中,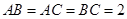 ,
,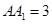 ,侧棱
,侧棱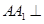 底面
底面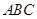 ,
,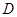 为
为 的中点,
的中点, 为
为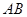 边上的动点。
边上的动点。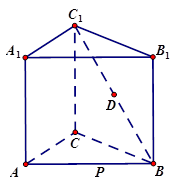
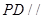 平面
平面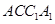
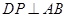 ,求四棱锥
,求四棱锥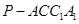 的体积。
的体积。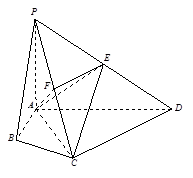
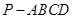 中,
中, ,
,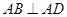 ,
,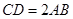 ,
, 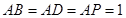 ,
,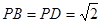 ,
,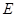 和
和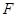 分别是
分别是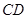 和
和 的中点.
的中点.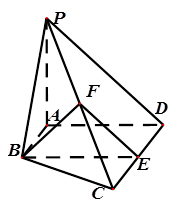
 底面
底面 ;
;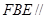 平面
平面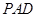 ;
;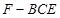 的体积.
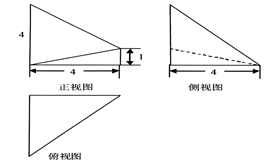
的体积.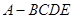 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.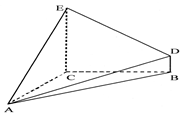
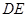 与
与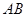 所成角的余弦值;
所成角的余弦值;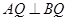 ,并说明理由.
,并说明理由.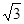 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.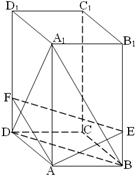
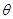 的正切值.
的正切值.