题目内容
如图,在棱长为1的正方体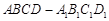 中.
中.
(1)求异面直线 与
与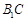 所成的角;
所成的角;
(2)求证平面 ⊥平面
⊥平面 .
.
(1)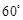 (2)先证
(2)先证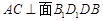 即可得证.
即可得证.
解析试题分析:
(1)如图, ∥
∥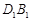 ,
,
则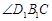 就是异面直线
就是异面直线 与
与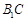 所成的角.
所成的角.
连接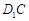 ,在
,在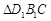 中,
中,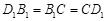 ,则
,则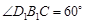 ,
,
因此异面直线 与
与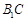 所成的角为
所成的角为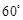 .
.
(2) 由正方体的性质可知  , 故
, 故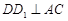 ,
,
又 正方形 中,
中,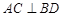 ,
,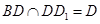 ∴
∴ 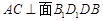 ;
;
又 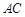
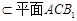 , ∴ 平面
, ∴ 平面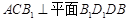 .
.
考点:向量语言表述面面的垂直、平行关系;用空间向量求直线间的夹角、距离.
点评:本题考查的知识点是向量语言表述直线的垂直关系,用空间向量求直线间的夹角,其中解法一(几
何法)的关键是熟练掌握空间线面关系的判定、性质及相互转换;解法二(向量法)的关键是建立恰当的
空间坐标系,将空间线面关系问题转化为向量夹角问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
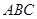 中,
中,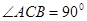 ,
,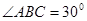 ,
,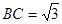 ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心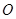 在边
在边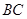 上,半圆与
上,半圆与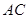 、
、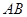 分别相切于点
分别相切于点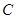 、
、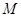 ,与
,与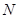 ),将△
),将△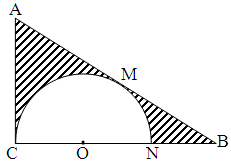
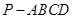 中,
中, ,
,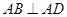 ,
,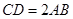 ,
, 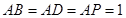 ,
,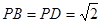 ,
,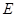 和
和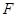 分别是
分别是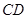 和
和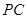 的中点.
的中点.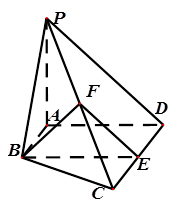
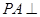 底面
底面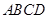 ;
;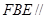 平面
平面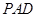 ;
;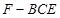 的体积.
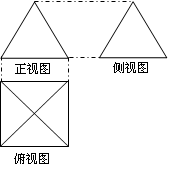
的体积.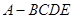 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.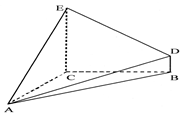
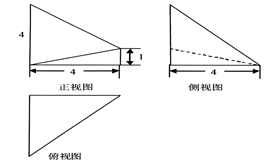
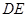 与
与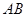 所成角的余弦值;
所成角的余弦值;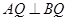 ,并说明理由.
,并说明理由. 的正三角形,O是底面圆心.
的正三角形,O是底面圆心.
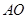 的中点
的中点 作平行于圆锥底面的截面,求截得的圆台的体积.
作平行于圆锥底面的截面,求截得的圆台的体积.
 ,且
,且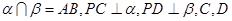 是垂足,
是垂足,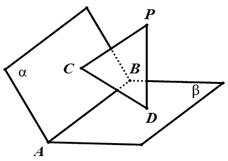
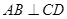
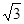 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.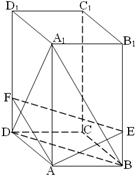
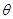 的正切值.
的正切值.