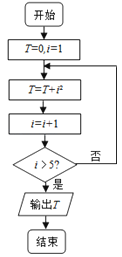
题目内容
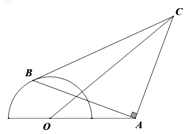
【题目】如图,半圆O的直径为2,A为直径延长线上一点,OA=2,B为半圆上任意一点,以线段AB为腰作等腰直角△ABC(C、O两点在直线AB的两侧),当∠AOB变化时,OC≤m恒成立,则m的最小值为______.
【答案】2![]() +1
+1
【解析】
根据题意,以O为坐标原点,OA为x轴建立坐标系,设∠AOB=θ,分析A、B的坐标,可得向量![]() 的坐标,又由△ABC为等腰直角三角形,则AC⊥AB且|AC|=|AB|,分析可得向量
的坐标,又由△ABC为等腰直角三角形,则AC⊥AB且|AC|=|AB|,分析可得向量![]() 的坐标,进而由向量坐标的加法可得向量
的坐标,进而由向量坐标的加法可得向量![]() 的坐标,进而可得向量
的坐标,进而可得向量![]() 的模,分析其最大值,若OC≤m恒成立,分析可得答案.
的模,分析其最大值,若OC≤m恒成立,分析可得答案.
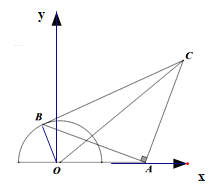
解:根据题意,以O为坐标原点,OA为x轴建立坐标系,如图:
则A(2,0),设∠AOB=θ,(0≤θ≤π),则B的坐标为(cosθ,sinθ),
则![]() =(cosθ-2,sinθ),
=(cosθ-2,sinθ),
△ABC为等腰直角三角形,则AC⊥AB且|AC|=|AB|,
又由C、O两点在直线AB的两侧,则![]() =(sinθ,2-cosθ),
=(sinθ,2-cosθ),
则![]() =(2+sinθ,2-cosθ),
=(2+sinθ,2-cosθ),
则|![]() |2=(2+sinθ)2+(2-cosθ)2=9+4(sinθ-cosθ)=9+4
|2=(2+sinθ)2+(2-cosθ)2=9+4(sinθ-cosθ)=9+4![]() sin(θ-
sin(θ-![]() ),
),
所以当θ=![]() 时,|
时,|![]() |2取得最大值9+4
|2取得最大值9+4![]() ,
,
则OC的最大值为2![]() +1,
+1,
若OC≤m恒成立,则m≥2![]() +1,即m的最小值为2
+1,即m的最小值为2![]() +1;
+1;
故答案为:2![]() +1.
+1.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】某中学将100名高一新生分成水平相同的甲、乙两个平行班,每班50人,某教师采用![]() 、
、![]() 两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.
两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.

(1)在乙班的20个个体中,从不低于86分的成绩中随机抽取2人,求抽出的两个人均“成绩优秀”的概率;
(2)由以上统计数据填写![]() 列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
甲班( | 乙班( | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |