题目内容
设双曲线的—个焦点为F,虚轴的—个端点为B，如果直线FB与该双曲线的一条渐近线垂直，那么此双曲线的离心率为
A． | B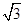． | C． | D． |
D
解析试题分析：设
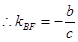
即
，
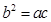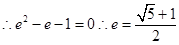
考点：求离心率
点评：求离心率的关键在于找到关于
的齐次方程或不等式
练习册系列答案
阅读快车系列答案
相关题目
已知抛物线的顶点在原点，焦点在y轴上，抛物线上的点
到焦点的距离等于5，
则m
A． | B． | C． | D． |
抛物线
的焦点坐标是( )
A． | B． | C．  | D． |
设抛物线y2 = 8x的准线与x轴交于点Q,若过点Q的直线
与抛物线有公共点,则直线的斜率的取值范围是（ ）
A．[－ ,] | B．[－2 , 2 ] | C．[－1 , 1 ] | D．[－4 , 4 ] |
过点(0，1)作直线，使它与抛物线y2=4x仅有一个公共点，这样的直线有( )
| A．1条 | B．2条 | C．3条 | D．4条 |
已知双曲线x2－
＝1的左顶点为A1，右焦点为F2，P为双曲线右支上一点，则
·
的最小值为( )
| A．－2 | B．－ | C．1 | D．0 |
等轴双曲线x2-y2=a2与直线y=ax(a>0)没有公共点，则a的取值范围( )
| A．a=1 | B．0<a<1 | C．a>1 | D．a≥1 |
的中心在原点,焦点在
轴上,
的准线交于
两点,
;则
(
)
，M,N是椭圆上关于原点对称的两点，P是椭圆上任意一点，且直线PM,PN的斜率分别为
，
=
，则椭圆的离心率为（ ）
