题目内容
若 、
、 是双曲线
是双曲线 的两焦点,点
的两焦点,点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,则
是等腰三角形,则 的周长为( )
的周长为( )
A. | B. | C. | D. |
D
解析试题分析:双曲线 可化为标准方程:
可化为标准方程: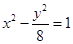 ,所以
,所以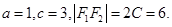 因为点
因为点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,所以
是等腰三角形,所以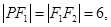 或
或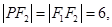 当
当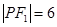 时,根据双曲线的定义有
时,根据双曲线的定义有 所以
所以 的周长为
的周长为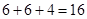 ;同理当
;同理当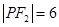 时,
时, 的周长为
的周长为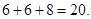
考点:本小题主要考查双曲线中基本量的计算和双曲线上点的性质以及双曲线定义的应用,考查了学生对问题的转化能力和运算求解能力.
点评:双曲线的定义在解题时有很重要的作用,要灵活应用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
下列曲线中,离心率为2的是( )
A. | B. | C. | D. |
过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
等轴双曲线x2-y2=a2与直线y=ax(a>0)没有公共点,则a的取值范围( )
| A.a=1 | B.0<a<1 | C.a>1 | D.a≥1 |
若点P是曲线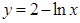 上任意一点,则点P到直线
上任意一点,则点P到直线 的最小距离是( )
的最小距离是( )
A.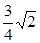 | B.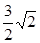 | C.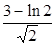 | D.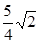 |
焦点坐标是 ,
, ,且虚轴长为
,且虚轴长为 的双曲线的方程是( )
的双曲线的方程是( )
A. | B. |
C. | D. |
短轴长为 ,离心率为
,离心率为 的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
| A.24 | B.12 | C.6 | D.3 |
 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上, 的准线交于
的准线交于 两点,
两点, ;则
;则

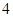

 的棱长为
的棱长为 ,点
,点 在棱
在棱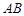 上, 且
上, 且 , 点
, 点 是平面
是平面 上的动点,且动点
上的动点,且动点 的距离与点
的距离与点