题目内容
下列命题中,真命题的个数为( )
①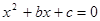 有一根大于1,另一根小于1的充要条件是
有一根大于1,另一根小于1的充要条件是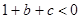
②当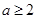 时,
时,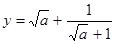 的最小值为1
的最小值为1
③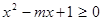 对于
对于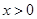 恒成立,则
恒成立,则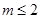
④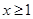 的一个充分不必要条件是
的一个充分不必要条件是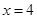
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:①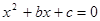 有一根大于1,另一根小于1的充要条件是
有一根大于1,另一根小于1的充要条件是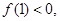 即
即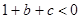 ,所以正确;②当
,所以正确;②当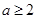 时,
时, 当且仅当
当且仅当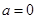 时取等号,因为
时取等号,因为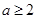 ,所以最小值取不到1,所以不正确;③
,所以最小值取不到1,所以不正确;③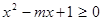 对于
对于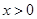 恒成立,所以
恒成立,所以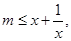 而
而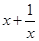 的最小值为2,所以
的最小值为2,所以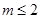 ,所以正确;④显然正确.
,所以正确;④显然正确.
考点:本小题主要考查方程根的分布问题、不等式恒成立问题、均值不等式的应用和充分、必要条件的判断,考查学生综合运用所学知识分析问题、解决问题的能力.
点评:方程根的分布问题要画图象辅助解决,不等式恒成立问题往往转化为求最值问题,利用均值不等式时要注意一正二定三相等三个条件缺一不可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
“AB>0”是“方程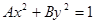 表示椭圆”的 ( )
表示椭圆”的 ( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知命题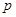 :
: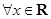 ,
,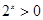 ,那么命题
,那么命题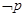 为( )
为( )
A.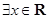 , ,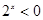 | B.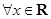 , ,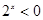 |
C.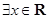 , ,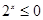 | D.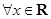 , ,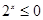 |
特称命题“存在一个被7整除的整数不是奇数”的否定是( )
| A.所有被7整除的整数都不是奇数 |
| B.所有奇数都不能被7整除 |
| C.所有被7整除的整数都是奇数 |
| D.存在一个奇数,不能被7整除 |
命题“存在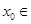 R,
R,
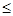 0”的否定是( )
0”的否定是( )
A.不存在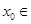 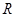 , ,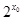 >0 >0 | B.存在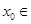 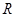 , , 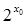 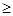 0 0 |
C.对任意的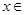 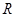 , , 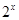 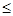 0 0 | D.对任意的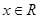 , ,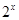 >0 >0 |
命题“?x>0,x2+x>0”的否定是( ).
A.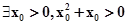 | B.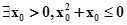 |
| C.?x>0,x2+x≤0 | D.?x≤0,x2+x>0 |
下列有关命题的说法正确的是
A.命题“若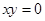 ,则 ,则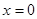 ”的否命题为:“若 ”的否命题为:“若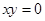 ,则 ,则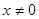 ” ” |
B.“若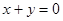 ,则 ,则 , ,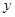 互为相反数”的逆命题为真命题 互为相反数”的逆命题为真命题 |
C.命题“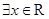 ,使得 ,使得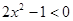 ”的否定是:“ ”的否定是:“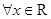 ,均有 ,均有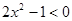 ” ” |
D.命题“若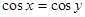 ,则 ,则 ”的逆否命题为真命题 ”的逆否命题为真命题 |
已知向量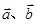 都是非零向量,“
都是非零向量,“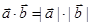 ”是“
”是“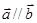 ”的( )
”的( )
| A.必要非充分条件. | B.充分非必要条件. |
| C.充要条件. | D.既非充分也非必要条件 |
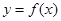 是幂函数,则函数
是幂函数,则函数